第42页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
11. [2025 湖州模拟] 如图, 以 $ AB $ 为斜边作等腰直角三角形 $ ABC $, 再以点 $ A $ 为圆心, $ AC $ 长为半径作弧, 交线段 $ AB $ 于点 $ P $, 则 $ AB:AP $ 等于 (
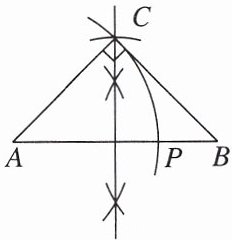
A.$\sqrt{2}:1$
B.$\sqrt{3}:1$
C.$\sqrt{3}:\sqrt{2}$
D.$ 3:2 $
A
)
A.$\sqrt{2}:1$
B.$\sqrt{3}:1$
C.$\sqrt{3}:\sqrt{2}$
D.$ 3:2 $
答案:
A
12. 已知三条线段的长分别为 $ 1 cm, 2 cm, \sqrt{2} cm $, 如果另外一条线段与它们是成比例线段, 那么另外一条线段的长为
2√2cm或√2/2cm或√2cm
.
答案:
2√2cm或√2/2cm或√2cm [点拨]设另外一条线段的长为a cm,
由题意,得1/2=√2/a或1/a=2/√2或a/1=2/√2或2/1=√2/a,
解得a=2√2或a=√2/2或a=√2.
由题意,得1/2=√2/a或1/a=2/√2或a/1=2/√2或2/1=√2/a,
解得a=2√2或a=√2/2或a=√2.
13. 小南在比例尺是 $ 1:100 $ 的房屋设计图上, 量得自家房屋平面图长 $ 15 cm $、宽 $ 9 cm $, 若把房屋的地面铺上边长为 $ 0.6 m $ 的正方形地砖, 一共需要
375
块地砖.
答案:
375
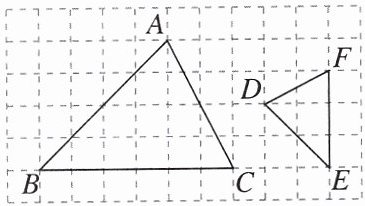
14. 已知 $ \triangle ABC $ 与 $ \triangle DEF $ 在网格中的位置如图所示, 如果每个小正方形的边长都是 1.
(1) 求 $\frac{AB}{DE}, \frac{BC}{EF}, \frac{AC}{DF}$ 的值;
(2) 求 $ \triangle ABC $ 的周长与 $ \triangle DEF $ 的周长之比;
(3) 在 $ AB, BC, AC, DE, EF, DF $ 这六条线段中, 指出其中三组成比例线段.
(1) 求 $\frac{AB}{DE}, \frac{BC}{EF}, \frac{AC}{DF}$ 的值;
(2) 求 $ \triangle ABC $ 的周长与 $ \triangle DEF $ 的周长之比;
(3) 在 $ AB, BC, AC, DE, EF, DF $ 这六条线段中, 指出其中三组成比例线段.

答案:
[解]
(1)由题意得AB=4√2,BC=6,AC=2√5,DE=2√2,EF=3,DF=√5,
∴AB/DE=2,BC/EF=2,AC/DF=2.
(2)由(Ⅰ)得AB/DE=BC/EF=AC/DF=₂,
∴(AB+BC+AC)/(DE+EF+DF)=(2DE+₂EF+2DF)/(DE+EF+DF)=2.
∴△ABC的周长与△DEF的周长之比为2:1.
(3)
∵AB/DE=BC/EF
∴ABDEBC,EF是成比例线段;
∵ABDE=AC/DF,
∴ABDEACDF是成比例线段;
∵BC/EF=AC/DF,
∴BCEFACDF是成比例线段id:23
answer:
(1)[解]以BF为公共边的“共边三角形”为△ABF,△DBF,△CBF.
由“共边三角形”的性质得S△DBF/S△CBF=BD/BC=1/2,S△ABF/S△DBF=AE/DE=1/1,
∴S△ABF:S△DBF:S△CBF=1:1:2.
∵△ABC的面积为45cm²,
∴S△DBF=S△ABF=1/3S△ABC=15cm²,
S△CBF=2/3S△ABC=30cm².
(2)[证明]由“共边三角形”的性质得S△ABF/S△CBF=AF/CF,
由
(1)得S△ABF/S△CBF=1/2,
∴AF/CF=1/2,
∴AF/AC=1/3,
∴AF=1/3AC.
(3)2:5 [点拨]由“共边三角形”的性质得S△DBF/S△CBF=BD/BC=2/5,S△ABF/S△DBF=AE/DE=1/1,
∴S△ABF:S△DBF:S△CBF=2:2:5.
∴S△ABF/S△CBF=AF/CF=2/5.
(1)由题意得AB=4√2,BC=6,AC=2√5,DE=2√2,EF=3,DF=√5,
∴AB/DE=2,BC/EF=2,AC/DF=2.
(2)由(Ⅰ)得AB/DE=BC/EF=AC/DF=₂,
∴(AB+BC+AC)/(DE+EF+DF)=(2DE+₂EF+2DF)/(DE+EF+DF)=2.
∴△ABC的周长与△DEF的周长之比为2:1.
(3)
∵AB/DE=BC/EF
∴ABDEBC,EF是成比例线段;
∵ABDE=AC/DF,
∴ABDEACDF是成比例线段;
∵BC/EF=AC/DF,
∴BCEFACDF是成比例线段id:23
answer:
(1)[解]以BF为公共边的“共边三角形”为△ABF,△DBF,△CBF.
由“共边三角形”的性质得S△DBF/S△CBF=BD/BC=1/2,S△ABF/S△DBF=AE/DE=1/1,
∴S△ABF:S△DBF:S△CBF=1:1:2.
∵△ABC的面积为45cm²,
∴S△DBF=S△ABF=1/3S△ABC=15cm²,
S△CBF=2/3S△ABC=30cm².
(2)[证明]由“共边三角形”的性质得S△ABF/S△CBF=AF/CF,
由
(1)得S△ABF/S△CBF=1/2,
∴AF/CF=1/2,
∴AF/AC=1/3,
∴AF=1/3AC.
(3)2:5 [点拨]由“共边三角形”的性质得S△DBF/S△CBF=BD/BC=2/5,S△ABF/S△DBF=AE/DE=1/1,
∴S△ABF:S△DBF:S△CBF=2:2:5.
∴S△ABF/S△CBF=AF/CF=2/5.
15. 新视角 新定义题 若有一条公共边的两个三角形称为 “共边三角形”. 如图 ①, $ \triangle ABC $ 与 $ \triangle ABD $ 是以 $ AB $ 为公共边的 “共边三角形”. “共边三角形” 的性质: 共边 $ \triangle ABC $ 与 $ \triangle ABD $, 连结第三个顶点 $ DC $ 并延长交 $ AB $ 于点 $ E $, 则 $\frac{S_{\triangle ABC}}{S_{\triangle ABD}}= \frac{CE}{DE}$.
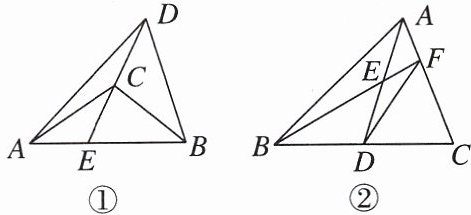
【问题解决】
如图②, 在 $ \triangle ABC $ 中, $ D $ 为 $ BC $ 的中点, $ E $ 为 $ AD $ 的中点, 连结 $ BE $ 并延长交 $ AC $ 于点 $ F $, 连结 $ DF $.
(1) 找出以 $ BF $ 为公共边的所有 “共边三角形”, 若 $ \triangle ABC $ 的面积为 $ 45 cm^2 $, 分别求出这些 “共边三角形” 的面积;
(2) 求证: $ AF = \frac{1}{3}AC $;
(3) 若将 “$ D $ 为 $ BC $ 的中点” 条件, 改为 “$ BD:DC = 2:3 $”, 则 $ AF:CF = $ .

【问题解决】
如图②, 在 $ \triangle ABC $ 中, $ D $ 为 $ BC $ 的中点, $ E $ 为 $ AD $ 的中点, 连结 $ BE $ 并延长交 $ AC $ 于点 $ F $, 连结 $ DF $.
(1) 找出以 $ BF $ 为公共边的所有 “共边三角形”, 若 $ \triangle ABC $ 的面积为 $ 45 cm^2 $, 分别求出这些 “共边三角形” 的面积;
以BF为公共边的“共边三角形”为:△ABF、△DBF、△CBF。面积分别为:15 cm²、15 cm²、30 cm²。
(2) 求证: $ AF = \frac{1}{3}AC $;
证明:∵△ABF与△CBF共顶点B,底边AF、FC在AC上,∴S△ABF/S△CBF=AF/CF。由(1)知S△ABF=15,S△CBF=30,∴15/30=AF/CF⇒AF/CF=1/2⇒AF=1/3AC。
(3) 若将 “$ D $ 为 $ BC $ 的中点” 条件, 改为 “$ BD:DC = 2:3 $”, 则 $ AF:CF = $ .
2:5
答案:
(1)
以BF为公共边的“共边三角形”为:△ABF、△DBF、△CBF。
∵D为BC中点,S△ABC=45,
∴S△ABD=S△ADC=22.5 cm²。
E为AD中点,
∴S△ABE=S△BDE=11.25 cm²。
设S△DEF=S△AEF=p,S△DBF=x,S△ABF=y。
由S△ABE=y-p=11.25,S△BDE=x-p=11.25,得y=x。
又S△ABF+S△CBF=45,S△CBF=2x(D为BC中点,S△DBF=S△DCF=x),
∴x+2x=45⇒x=15,y=15,S△CBF=30。
面积分别为:15 cm²、15 cm²、30 cm²。
(2)
证明:
∵△ABF与△CBF共顶点B,底边AF、FC在AC上,
∴S△ABF/S△CBF=AF/CF。
由
(1)知S△ABF=15,S△CBF=30,
∴15/30=AF/CF⇒AF/CF=1/2⇒AF=1/3AC。
(3)
2:5
(1)
以BF为公共边的“共边三角形”为:△ABF、△DBF、△CBF。
∵D为BC中点,S△ABC=45,
∴S△ABD=S△ADC=22.5 cm²。
E为AD中点,
∴S△ABE=S△BDE=11.25 cm²。
设S△DEF=S△AEF=p,S△DBF=x,S△ABF=y。
由S△ABE=y-p=11.25,S△BDE=x-p=11.25,得y=x。
又S△ABF+S△CBF=45,S△CBF=2x(D为BC中点,S△DBF=S△DCF=x),
∴x+2x=45⇒x=15,y=15,S△CBF=30。
面积分别为:15 cm²、15 cm²、30 cm²。
(2)
证明:
∵△ABF与△CBF共顶点B,底边AF、FC在AC上,
∴S△ABF/S△CBF=AF/CF。
由
(1)知S△ABF=15,S△CBF=30,
∴15/30=AF/CF⇒AF/CF=1/2⇒AF=1/3AC。
(3)
2:5
查看更多完整答案,请扫码查看


