《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

9. 如图,$AB$,$CD是\odot O$的两条弦,且$AB = CD$. $OM\perp AB$,$ON\perp CD$,垂足分别为$M$,$N$,$BA$,$DC的延长线交于点P$,连结$OP$. 下列结论：①$\overset{\frown}{AB}= \overset{\frown}{CD}$；②$OM = ON$；③$PA = PC$；④$\angle BPO = \angle DPO$. 其中正确的有(D)

A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： D 【点拨】
∵AB=CD,
∴$\overset{\frown}{AB}$=$\overset{\frown}{CD}$,故①正确；
∵OM⊥AB,ON⊥CD，
∴AM=MB=$\frac{1}{2}$AB,CN=ND=$\frac{1}{2}$CD,OM=ON，故②正确.
∵OP=OP,OM=ON,
∴Rt△OPM≌Rt△OPN，
∴PM=PN,∠BPO=∠DPO,故④正确；
∵AM=CN,
∴PA=PC,故③正确.
综上可知,正确的有 4 个.

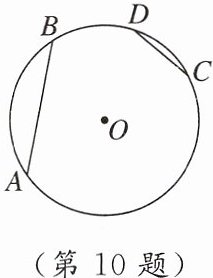
10. 如图,在$\odot O$中,满足$\overset{\frown}{AB}= 2\overset{\frown}{CD}$,若$AB = 6$,则$CD$的长可能是( )

A.$1$
B.$2$
C.$3$
D.$4$

答案：
D 【点拨】如图,取$\overset{\frown}{AB}$的中点 E,连结 OE 交 AB 于 F,连结 BE.
∵E 为$\overset{\frown}{AB}$的中点,AB=6,
∴$\overset{\frown}{AB}$=2$\overset{\frown}{EB}$,BF=$\frac{1}{2}$AB=3,OE⊥AB，

∴BE＞BF,即 BE＞3，
∵$\overset{\frown}{AB}$=2$\overset{\frown}{CD}$,
∴$\overset{\frown}{CD}$=$\overset{\frown}{EB}$,
∴CD=BE＞3，
∴CD 的长可能是 4.

11. 如图,$AB为\odot O$的直径,点$C是\overset{\frown}{BE}$的中点,过点$C作CD\perp AB于点F$,交$\odot O于点D$,若$BE = 6$,$BF = 1$,则$\odot O$的半径长是( )

A.$\sqrt{10}$
B.$4$
C.$5$
D.$\frac{16}{3}$

答案：
C 【点拨】如图,连结 OD,设⊙O 的半径为 r.
∵CD⊥AB,AB 为⊙O 的直径，
∴$\overset{\frown}{BC}$=$\overset{\frown}{BD}$,CF=DF.
∵点 C 是$\overset{\frown}{BE}$的中点,
∴$\overset{\frown}{CE}$=$\overset{\frown}{CB}$，
∴$\overset{\frown}{BE}$=$\overset{\frown}{CD}$,
∴CD=BE=6,
∴DF=$\frac{1}{2}$CD=3.
∵BF=1,OB=r,
∴OF=r - 1,
∴$3^{2}+(r - 1)^{2}$=$r^{2}$,解得 r=5.
∴⊙O 的半径长是 5.

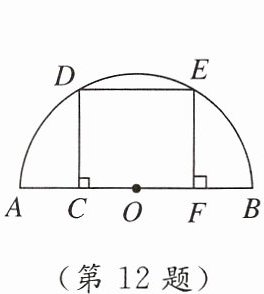
12. 新趋势 学科内综合 如图,在以$AB$为直径的半圆中,$\overset{\frown}{AD}= \overset{\frown}{EB}$,$CD\perp AB$,$EF\perp AB$,$CD = CF = 1$,则以$AC和BC$的长为两根的一元二次方程是$x^{2}-\sqrt{5}x+1=0$.

答案： $x^{2}-\sqrt{5}x+1=0$ 【点拨】连结 OD,OE. 根据题意,易证明 Rt△DOC≌Rt△EOF,所以 CO=FO=$\frac{1}{2}$,在 Rt△DOC 中，DO=$\sqrt{1^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{5}}{2}$. 所以 AO=DO=$\frac{\sqrt{5}}{2}$,AC=$\frac{\sqrt{5}-1}{2}$,AB=2DO=$\sqrt{5}$. 所以 BC=AB - AC=$\sqrt{5}-\frac{\sqrt{5}-1}{2}$=$\frac{\sqrt{5}+1}{2}$,所以以 AC 和 BC 的长为两根的一元二次方程是$(x-\frac{\sqrt{5}-1}{2})(x-\frac{\sqrt{5}+1}{2})$=0. 整理,得$x^{2}-\sqrt{5}x+1=0$.

13. 如图,已知半圆$O的直径AB为3$,弦$AC与弦BD交于点E$,$OD\perp AC$,垂足为$F$,$AC = BD$,则弦$AC$的长为______.

答案：
$\frac{3\sqrt{3}}{2}$ 【点拨】如图,连结 OC.
∵OD⊥AC，
∴$\overset{\frown}{AD}$=$\overset{\frown}{CD}$,∠AFO=90°.
∵AC=BD,
∴$\overset{\frown}{AC}$=$\overset{\frown}{BD}$,即$\overset{\frown}{AD}$+$\overset{\frown}{CD}$=$\overset{\frown}{CD}$+$\overset{\frown}{BC}$.
∴$\overset{\frown}{AD}$=$\overset{\frown}{BC}$.
∴$\overset{\frown}{AD}$=$\overset{\frown}{CD}$=$\overset{\frown}{BC}$.
∴∠AOD=∠DOC=∠BOC=60°.
∵AB=3,
∴AO=BO=$\frac{3}{2}$.
∵在 Rt△AOF 中,∠OAF=90° - ∠AOD=30°，
∴OF=$\frac{1}{2}$AO=$\frac{3}{4}$.
由勾股定理,得 AF=$\sqrt{AO^{2}-OF^{2}}$=$\sqrt{(\frac{3}{2})^{2}-(\frac{3}{4})^{2}}$=$\frac{3\sqrt{3}}{4}$,
∴AC=2AF=$\frac{3\sqrt{3}}{2}$.

14. 如图,在$\odot O$中,$C为\overset{\frown}{AB}$的中点,$CD\perp OA于点D$,$CE\perp OB于点E$.
(1) 求证：$CD = CE$.
(2) 若$\angle AOB = 120^{\circ}$,$OA = 6$,求四边形$DOEC$的面积.

答案：
（1）【证明】如图,连结 OC.
∵C 为$\overset{\frown}{AB}$的中点，
∴$\overset{\frown}{AC}$=$\overset{\frown}{BC}$，
∴∠AOC=∠BOC，
∴OC 平分∠AOB.
又
∵CD⊥OA,CE⊥OB，
∴CD=CE.
（2）【解】
∵∠AOB=120°,∠AOC=∠BOC，
∴∠AOC=60°.
∵∠CDO=90°,
∴∠OCD=30°.
在 Rt△ODC 中,OD=$\frac{1}{2}$OC=3，
∴CD=$\sqrt{OC^{2}-OD^{2}}$=3$\sqrt{3}$，
∴$S_{\triangle CDO}$=$\frac{1}{2}$OD·CD=$\frac{9\sqrt{3}}{2}$.
同理,可得$S_{\triangle CEO}$=$\frac{9\sqrt{3}}{2}$，
∴$S_{四边形 DOEC}$=$S_{\triangle CDO}$+$S_{\triangle CEO}$=9$\sqrt{3}$.

15. 如图,$AB是半圆O$的直径,$C$是半圆上的一点(不与点$A$,$B$重合),过点$A作AD// OC交半圆于点D$,$E是直径AB$上的一点,且$AE = AD$,连结$CE$,$CD$.
(1) 求证：$CD = CE$.
(2) 如果$\overset{\frown}{AD}= 3\overset{\frown}{CD}$,延长$EC$,$AD相交于点F$,连结$OD$. 求证：四边形$OCFD$是菱形.

答案：
【证明】（1）如图①,连结 AC.
∵OA=OC,
∴∠OAC=∠OCA.
∵AD//OC,
∴∠DAC=∠OCA，
∴∠DAC=∠OAC，
在△DAC 和△EAC 中，
$\begin{cases}AD=AE,\\\angle DAC=\angle EAC,\\AC=AC,\end{cases}$
∴△DAC≌△EAC(SAS),
∴CE=CD.
（2）如图②,连结 CA.
∵$\overset{\frown}{AD}$=3$\overset{\frown}{CD}$,
∴∠AOD=3∠COD.
∵AD//OC,
∴∠ADO=∠DOC.
∵OA=OD,
∴∠OAD=∠ODA.
∵∠AOD+∠OAD+∠ADO=180°，
∴5∠ADO=180°,
∴∠ADO=36°，
∴∠AOD=108°,∠DOC=36°.
∵OD=OC,
∴∠ODC=72°,
∴∠ADC=108°.
∵△DAC≌△EAC,
∴∠ADC=∠AEC=108°，
∴∠AOD=∠AEC,
∴OD//CE.
又
∵OC//AD，
∴四边形 OCFD 是平行四边形.
又
∵OD=OC,
∴平行四边形 OCFD 是菱形.