《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

15. 新趋势·跨学科 如图,嘉嘉同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜. 手电筒的灯泡在点$G$处,手电筒的光从平面镜上的点$B$处反射后,恰好经过木板的边缘点$F$,落在墙上的点$E$处,点$E到地面的高度DE = 3.5m$,点$F到地面的高度CF = 1.5m$,灯泡到木板的水平距离$AC = 5.4m$,墙到木板的水平距离$CD = 4m$. 已知光在镜面反射中的入射角等于反射角,图中点$A$,$B$,$C$,$D$在同一水平面上.
(1)求$BC$的长；
(2)求灯泡到地面的高度$AG$.

答案： [解]
(1)由题意得FC//DE,则△BFC∽△BED,
∴$\frac{BC}{BD}=\frac{FC}{DE}$,即$\frac{BC}{BC+4}=\frac{1.5}{3.5}$,解得BC=3m,
∴BC的长为3m.　　
(2)
∵AC=5.4m,BC=3m,
∴AB=5.4−3=2.4(m).
∵光在镜面反射中的入射角等于反射角,
∴易得∠GBA=∠FBC.　　由题意知∠GAB=∠FCB=90°,
∴△BGA∽△BFC.
∴$\frac{AG}{FC}=\frac{AB}{BC}$.
∴$\frac{AG}{1.5}=\frac{2.4}{3}$,解得AG=1.2m,
∴灯泡到地面的高度AG为1.2m.

16. $[2025宁波鄞州区期末]$如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD\perp AB于点D$,矩形$GDEF$,矩形$MNHD的顶点分别在\triangle ACD$,$\triangle BCD$的三边上,且矩形$GDEF\sim矩形MNHD$,则两矩形的相似比是(D)

A.$\frac{AC}{AB}$
B.$\frac{CE}{EH}$
C.$\frac{CH}{CD}$
D.$\frac{CD}{BD}$

答案： D

17. 如图,在$□ FBCE$中,点$J$,$G分别在边BC$,$EF$上,$JG// BF$,四边形$ABCD\sim四边形HGF A$,相似比$k = 3$,则下列一定能求出$\triangle BIJ$面积的条件是(C)

A.四边形$HDEG和四边形AHGF$的面积之差
B.四边形$ABCD和四边形HDEG$的面积之差
C.四边形$ABCD和四边形ADEF$的面积之差
D.四边形$JCDH和四边形HDEG$的面积之差

答案： C　　[点拨]
∵四边形FBCE是平行四边形,
∴BF//CE.　　如图,过点A作AM//EF交CE于点M,过点D作DN//BC交BF于点N,　　易得四边形AFEM，四边形BJGF，四边形BCDN是平行四边形，
∴AF=ME，FG=BJ.
∵四边形ABCD∽四边形HGFA，相似比k=3，
∴CD=3AF=3ME，　　BC=3FG=3BJ，　　易得S□BCDN=3S□MEFA=2S△BCD.
∵JG//BF，
∴JG//CE.
∴△BCD∽△BJI，且相似比是3.
∴9S△BJI=S△BCD.　　易知S△ADN=S△ADM，
∴S四边形ABCD-S□BCDN=S四边形ADEF-S□MEFA，
∴S四边形ABCD-S四边形ADEF=S□BCDN-S□MEFA=$\frac{4}{3}S_{\triangle BCD}=12S_{\triangle BJI}$.

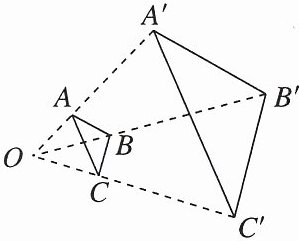
18. 如图,$\triangle ABC和\triangle A'B'C'是以点O$为位似中心的位似图形,点$A在线段OA'$上. 若$OA:AA' = 1:2$,则$\triangle ABC和\triangle A'B'C'$的周长之比为1:3.

答案： 1:3

19. 如图,在$6×6$的方格纸上,以点$A$为位似中心,作$\triangle ABC的位似图形\triangle AEF$,并把$\triangle ABC的边长扩大为原来的2$倍.

答案：
[解]如图,△AEF即为所求.