《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

8. 在一个不透明的箱子里装有 $ m $ 个球,其中红球 $ 4 $ 个,这些球除颜色外都相同,每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回,大量重复试验后发现,摸到红球的频率在 $ 0.2 $,那么可以估算出 $ m $ 的值为20。

答案： 20

9. 有四张分别画有线段、等边三角形、平行四边形和正方形的卡片,它们的背面都相同. 现将它们背面朝上,从中翻开任意一张卡片,其上的图形是中心对称图形,但不是轴对称图形的概率是(A)
A.$ \frac{1}{4} $
B.$ \frac{1}{2} $
C.$ \frac{3}{4} $
D.$ 1 $

答案： A

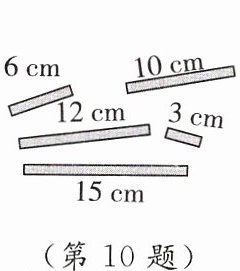
10. 新趋势 学科内综合 小芳同学有两根长度为 $ 4 \, cm $,$ 10 \, cm $ 的木棒,她想钉一个三角形相框,桌上有五根木棒供她选择(如图所示),从中任选一根,与原来的两根木棒能钉成三角形相框的概率是$\frac{2}{5}$。

答案： $\frac{2}{5}$

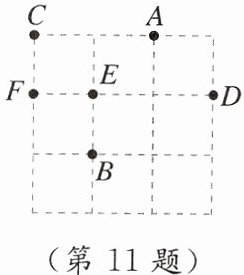
11. 如图,在 $ 3 × 3 $ 的方格中,点 $ A $,$ B $,$ C $,$ D $,$ E $,$ F $ 分别位于格点上,从 $ C $,$ D $,$ E $,$ F $ 四点中任取一点,与点 $ A $,$ B $ 为顶点作三角形,则所作三角形为等腰三角形的概率是$\frac{3}{4}$。

答案： $\frac{3}{4}$

12. 有七张正面分别标有数字 $ -3 $,$ -2 $,$ -1 $,$ 0 $,$ 1 $,$ 2 $,$ 3 $ 的卡片,它们除数字不同外其余全部相同. 现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为 $ a $. 请解答下列问题：
(1) 关于 $ x $ 的一元二次方程 $ (a - 3)x^2 - 2(a - 1)x + a = 0 $ 有两个不相等的实数根的概率是$\frac{3}{7}$；
(2) 以 $ x $ 为自变量的二次函数 $ y = ax^2 - (a^2 + 2)x + 2 $ 的图象经过点 $ (1, 0) $ 的概率是$\frac{1}{7}$。

答案：
(1)$\frac{3}{7}$；
(2)$\frac{1}{7}$

13. 一个不透明的袋中装有红、黄、白三种颜色的球共 $ 100 $ 个,它们除颜色外都相同,其中黄球的数量比白球的 $ 3 $ 倍多 $ 10 $ 个. 已知从袋中摸出一个球是红球的概率是 $ 0.3 $。
(1) 求袋中红球的数量；
(2) 求从袋中摸出一个球是白球的概率；
(3) 取走 $ 5 $ 个球(其中没有红球),求从剩余的球中摸出一个球是红球的概率。

答案： 【解】
(1)$100×0.3=30$(个).所以袋中红球的数量为30个.
(2)设白球有x个,则黄球有$(3x+10)$个,根据题意得$x+3x+10=100-30$,解得$x=15$.所以从袋中摸出一个球是白球的概率为$\frac{15}{100}=\frac{3}{20}$.
(3)因为取走5个球后,还剩95个球,其中红球的个数没有发生变化,所以从剩余的球中摸出一个球是红球的概率为$\frac{30}{95}=\frac{6}{19}$.

14. 从 $ -3 $,$ -2 $,$ -1 $,$ 0 $,$ 1 $ 这五个数中,随机取出一个数,记为 $ a $,求出 $ a $ 使得关于 $ x $ 的不等式组 $ \begin{cases} x - a \leq 0 \\ x - 5 ＜ 3(x - 2) \end{cases} $ 无解,且使得关于 $ x $ 的分式方程 $ \frac{x - 1}{x - 2} - \frac{a}{2 - x} = 3 $ 有整数解的概率。

答案： 【解】$\begin{cases}x-a\leqslant0,\textcircled{1}\\x-5＜3(x-2),\textcircled{2}\end{cases}$由①,得$x\leqslant a$;由②,得$x＞\frac{1}{2}$.所以当a取-3,-2,-1,0时,不等式组无解.解分式方程$\frac{x-1}{x-2}-\frac{a}{2-x}=3$,得$x=\frac{a+5}{2}$,所以当a取-3,1时,$\frac{a+5}{2}$是整数;当a取-1时,$x=2$是增根.综上,只有a取-3才符合题意,所以所求概率为$\frac{1}{5}$.