第54页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 相似多边形的定义:对应角
相等
,对应边成比例
的两个多边形叫做相似多边形,相似多边形对应边
的比叫做相似比.
答案:
相等;成比例;对应边
2. 相似多边形的性质:相似多边形的周长之比等于
相似比
,面积之比等于相似比的平方
.
答案:
相似比;相似比的平方
1. 观察下列每组图形,是相似图形的是(

C
)
答案:
C
2. 两个多边形相似的条件是(
A.对应角相等
B.对应边成比例
C.对应角相等或对应边成比例
D.对应角相等且对应边成比例
D
)A.对应角相等
B.对应边成比例
C.对应角相等或对应边成比例
D.对应角相等且对应边成比例
答案:
D
3. 如图,在梯形$ABCD$中,$E$,$F分别为AB$,$DC$两腰上的点,且$EF// BC$. 若$AE = 2$,$AB = 5$,且梯形$AEFD与梯形EBCF$相似,则梯形$AEFD与梯形EBCF$的周长比是(
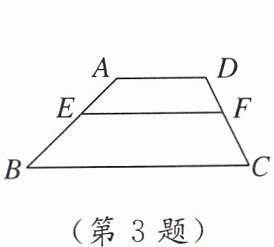
A.$2:3$
B.$3:2$
C.$4:9$
D.$9:4$
A
)
A.$2:3$
B.$3:2$
C.$4:9$
D.$9:4$
答案:
A
4. 如图,六边形$ABCDEF\sim六边形GHIJKL$,相似比为$2:1$,下列结论中,正确的是(
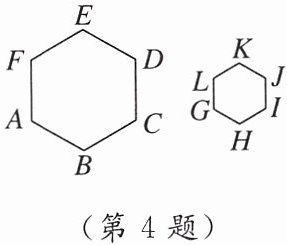
A.$\angle E = 2\angle K$
B.$BC = 2IJ$
C.$C_{六边形ABCDEF} = C_{六边形GHIJKL}$
D.$S_{六边形ABCDEF} = 4S_{六边形GHIJKL}$
D
)
A.$\angle E = 2\angle K$
B.$BC = 2IJ$
C.$C_{六边形ABCDEF} = C_{六边形GHIJKL}$
D.$S_{六边形ABCDEF} = 4S_{六边形GHIJKL}$
答案:
D
5. $[2025杭州高桥中学月考]制作一块3m×2m长方形广告牌的成本是120$元,在每平方米制作成本相同的情况下,若将此广告牌的四边都扩大为原来的$3$倍,那么扩大后长方形广告牌的成本是(
A.$360$元
B.$720$元
C.$1080$元
D.$3240$元
C
)A.$360$元
B.$720$元
C.$1080$元
D.$3240$元
答案:
C [点拨]
∵3×2=6(m²),制作一块3m×2m长方形广告牌的成本是120元,
∴长方形广告牌的成本是120÷6=20(元/m²). 将此广告牌的四边都扩大为原来的3倍, 则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54(m²).
∴扩大后长方形广告牌的成本는54×20=1080(元).
∵3×2=6(m²),制作一块3m×2m长方形广告牌的成本是120元,
∴长方形广告牌的成本是120÷6=20(元/m²). 将此广告牌的四边都扩大为原来的3倍, 则面积扩大为原来的9倍,
∴扩大后长方形广告牌的面积=9×6=54(m²).
∴扩大后长方形广告牌的成本는54×20=1080(元).
6. 如图,五边形$ABCDE\sim五边形A'B'C'D'E'$,则$\frac{BC}{B'C'}= $

2
.
答案:
2
7. 在一张比例尺为$1:10000$的地图上,一个多边形地区的周长为$80cm$,面积为$350cm^2$,则这个地区的实际周长为
8
$km$,实际面积为3.5
$km^2$.
答案:
8;3.5
8. 母题 教材$P152作业题T1$ 如图,四边形$ABCD\sim四边形A'B'C'D'$,求边$x$,$y的长度和角\alpha$的大小.


答案:
[解]
∵四边形ABCD∽四边形A'B'C'D',
∴$\frac{BC}{B'C'}=\frac{AB}{A'B'}=\frac{AD}{A'D'}$ ∠C=∠C'=α,∠D=∠D'=140°.
∴$\frac{x}{8}=\frac{y}{10}=\frac{9}{6}$,α=360°−∠A−∠B−∠D=360°−62°−75°−140°=83°.
∴x=12,y=15.
∵四边形ABCD∽四边形A'B'C'D',
∴$\frac{BC}{B'C'}=\frac{AB}{A'B'}=\frac{AD}{A'D'}$ ∠C=∠C'=α,∠D=∠D'=140°.
∴$\frac{x}{8}=\frac{y}{10}=\frac{9}{6}$,α=360°−∠A−∠B−∠D=360°−62°−75°−140°=83°.
∴x=12,y=15.
查看更多完整答案,请扫码查看


