第43页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
两条直线被一组平行线(不少于 3 条)所截,所得的
对应线段
成比例.
答案:
对应线段
1. 母题 教材 P126 作业题 T1 如图,直线 $ AB // CD // EF $, $ BD = 2 $, $ DF = 4 $,则 $ \frac{AC}{AE} = $(

A.$ \frac{1}{3} $
B.$ \frac{1}{2} $
C.$ \frac{2}{3} $
D.1
A
)
A.$ \frac{1}{3} $
B.$ \frac{1}{2} $
C.$ \frac{2}{3} $
D.1
答案:
A
2. 如图, $ DE // BC $, $ AD:BD = 2:3 $, $ EC = 12 $,则 $ AE $的长是(

A.6
B.8
C.12
D.20
B
)
A.6
B.8
C.12
D.20
答案:
B
3. 如图是一张书法练习纸,其中的竖格线都互相平行,且相邻两条格线间的距离都相等,不同竖格线上的三点 $ A $, $ B $, $ C $在同一直线上,若线段 $ AB = 3\mathrm{cm} $,则线段 $ BC $的长为(

A.$ 3\mathrm{cm} $
B.$ 4.5\mathrm{cm} $
C.$ 6\mathrm{cm} $
D.$ 9\mathrm{cm} $
B
)
A.$ 3\mathrm{cm} $
B.$ 4.5\mathrm{cm} $
C.$ 6\mathrm{cm} $
D.$ 9\mathrm{cm} $
答案:
B
4. 母题 教材 P125 例 1 如图,直线 $ AD $, $ BC $交于点 $ O $, $ AB // EF // CD $.若 $ AO = 2 $, $ OF = 1 $, $ FD = 2 $,则 $ \frac{BE}{EC} $的值为

$\frac{3}{2}$
.
答案:
$\frac{3}{2}$
5. 如图,在 $ \triangle ABC $中, $ D $为 $ BC $的中点,连结 $ AD $, $ E $为 $ AD $的中点,直线 $ BE $交 $ AC $于点 $ F $.
求证: $ AC = 3AF $.

求证: $ AC = 3AF $.

答案:
[证明]如图,取CF的中点G,连结DG,则FG=GC,又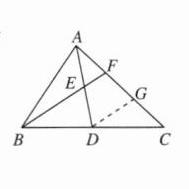
∵BD=DC,
∴DG//BF.
∴AE:ED=AF:FG.
∵AE=ED,
∴AF=FG.
∴AC=3AF.
[证明]如图,取CF的中点G,连结DG,则FG=GC,又

∵BD=DC,
∴DG//BF.
∴AE:ED=AF:FG.
∵AE=ED,
∴AF=FG.
∴AC=3AF.
6. 小明按照以下步骤画线段 $ AB $的三等分点:

这一画图过程体现的数学依据是(
A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例

这一画图过程体现的数学依据是(
D
)A.两直线平行,同位角相等
B.两条平行线之间的距离处处相等
C.垂直于同一条直线的两条直线平行
D.两条直线被一组平行线所截,所得的对应线段成比例
答案:
D
7. 母题 教材 P126 作业题 T4 作图题:请用直尺和圆规将如图所示的线段分成 $ 3:2 $ 的两条线段.要求:不写作法,但需保留作图痕迹.

答案:


8. 在 $ \triangle ABC $中, $ AB = 6 $, $ AC = 9 $,点 $ P $是直线 $ AB $上一点,且 $ AP = 2 $,过点 $ P $作 $ BC $边的平行线,交直线 $ AC $于点 $ M $,则 $ CM $的长为______.
答案:
6或12 [点拨]如图①,当点P在边AB上时,
∵AB=6,AP=2,
∴BP=AB - AP=6 - 2=4.
∵PM//BC,
∴$\frac{BP}{AB}=\frac{CM}{AC}$,即$\frac{4}{6}=\frac{CM}{9}$.
∴CM=6;如图②,当点P在BA的延长线上时,
∵AB=6,AP=2,
∴BP=AB + AP=6 + 2=8.
∵PM//BC,
∴$\frac{BP}{AB}=\frac{CM}{AC}$,即$\frac{8}{6}=\frac{CM}{9}$.
∴CM=12.综上,CM的长为6或12.
6或12 [点拨]如图①,当点P在边AB上时,
∵AB=6,AP=2,

∴BP=AB - AP=6 - 2=4.
∵PM//BC,
∴$\frac{BP}{AB}=\frac{CM}{AC}$,即$\frac{4}{6}=\frac{CM}{9}$.
∴CM=6;如图②,当点P在BA的延长线上时,
∵AB=6,AP=2,
∴BP=AB + AP=6 + 2=8.
∵PM//BC,
∴$\frac{BP}{AB}=\frac{CM}{AC}$,即$\frac{8}{6}=\frac{CM}{9}$.
∴CM=12.综上,CM的长为6或12.
查看更多完整答案,请扫码查看


