第29页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,$\odot O$的半径为5,弦$AB = 8$,$P是弦AB$上的一个动点,则$OP$的长度范围是(
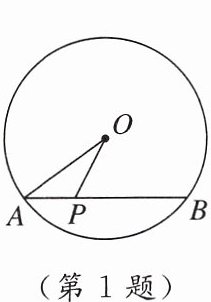
A.$8\leqslant OP\leqslant 10$
B.$5\leqslant OP\leqslant 8$
C.$4\leqslant OP\leqslant 5$
D.$3\leqslant OP\leqslant 5$
D
)
A.$8\leqslant OP\leqslant 10$
B.$5\leqslant OP\leqslant 8$
C.$4\leqslant OP\leqslant 5$
D.$3\leqslant OP\leqslant 5$
答案:
D
2. 如图,半径为5的$\odot A与y轴交于点B(0,2)$,$C(0,10)$,则点$A$的横坐标为(

A.3
B.4
C.5
D.6
A
)
A.3
B.4
C.5
D.6
答案:
A
3. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 3$,$BC = 4$,以点$C$为圆心,$CA长为半径的圆与AB交于点D$,则$AD$的长为(
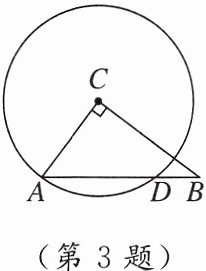
A.$\frac{9}{5}$
B.$\frac{21}{5}$
C.$\frac{18}{5}$
D.$\frac{5}{2}$
C
)
A.$\frac{9}{5}$
B.$\frac{21}{5}$
C.$\frac{18}{5}$
D.$\frac{5}{2}$
答案:
C
4. 新考法 分类讨论法 已知$\odot O的直径CD = 10$,$AB是\odot O$的弦,$AB = 8$,且$AB\perp CD于M$,则$AC$的长为(
A.$2\sqrt{5}$
B.$4\sqrt{5}$
C.$2\sqrt{5}或4\sqrt{5}$
D.$2\sqrt{3}或4\sqrt{3}$
C
)A.$2\sqrt{5}$
B.$4\sqrt{5}$
C.$2\sqrt{5}或4\sqrt{5}$
D.$2\sqrt{3}或4\sqrt{3}$
答案:
C
5. 新考向 传统文化 我国明代科学家徐光启在《农政全书》中描绘了一种我国古代常用的水利灌溉工具——筒车。如图,筒车盛水桶的运行轨道是以轴心$O$为圆心的圆,已知圆心$O$在水面的上方,$\odot O被水面截得的弦AB$长为16米,水面到运行轨道最低点的距离为4米,则$\odot O$的半径为
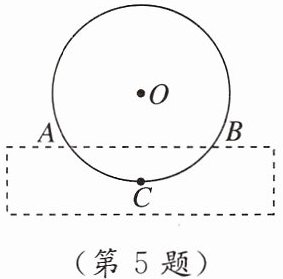
10
米。
答案:
10
6. 如图,$OA = OB$,$AB交\odot O于点C$,$D$,$OE$是半径,且$OE\perp AB于点F$。
(1)求证:$AC = BD$;
(2)若$CD = 6$,$EF = 1$,求$\odot O$的半径。
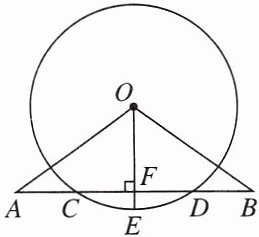
(1)求证:$AC = BD$;
(2)若$CD = 6$,$EF = 1$,求$\odot O$的半径。

答案:
(1)【证明】
∵OE⊥AB,CD为⊙O的弦,
∴CF=DF.
∵OA=OB,OE⊥AB,
∴AF=BF,
∴AF - CF=BF - DF,
即AC=BD.
(2)【解】如图,连结OC.
∵OE⊥AB,CD=6,CF=DF,
∴CF=$\frac{1}{2}$CD=3,∠OFC=90°,
∴CO²=CF²+OF².
设⊙O的半径是r,则OF=r - 1,
∴r²=3²+(r - 1)²,
解得r=5.
∴⊙O的半径是5.
∵OE⊥AB,CD为⊙O的弦,
∴CF=DF.
∵OA=OB,OE⊥AB,
∴AF=BF,
∴AF - CF=BF - DF,
即AC=BD.
(2)【解】如图,连结OC.
∵OE⊥AB,CD=6,CF=DF,
∴CF=$\frac{1}{2}$CD=3,∠OFC=90°,
∴CO²=CF²+OF².
设⊙O的半径是r,则OF=r - 1,
∴r²=3²+(r - 1)²,
解得r=5.
∴⊙O的半径是5.
7. 如图,在$\odot O$中,弦$AB// CD$,$AB = 8$,$CD = 6$,$AB$,$CD$之间的距离为1。
(1)求$\odot O$的半径;
(2)将弦$AB绕着圆心O$旋转一周,求弦$AB$扫过的面积。(结果保留$\pi$)
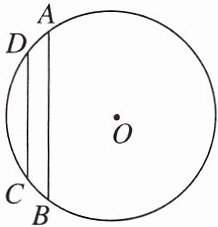
(1)求$\odot O$的半径;
(2)将弦$AB绕着圆心O$旋转一周,求弦$AB$扫过的面积。(结果保留$\pi$)

答案:
【解】(1)如图,过点O作OF⊥CD于点F,交AB于点E,连结OA,OD,则DF=CF=$\frac{1}{2}$OD=3.
∵AB//CD,
∴OE⊥AB,
∴AE=BE=$\frac{1}{2}$AB=4.设OE=x,则OF=x + 1.在
Rt△AEO中,OA²=OE²+AE²=x²+4²,
在Rt△DFO中,OD²=OF²+DF²=(x + 1)²+3².
∵OA=OD,
∴x²+4²=(x + 1)²+3²,解得x=3,
∴OD=OA=$\sqrt{3^{2}+4^{2}}$=5,即⊙O的半径为5.
(2)将弦AB绕着圆心O旋转一周,得到的图形是以点O为圆心,3为半径的圆与以点O为圆心,5为半径的圆所围成的圆环,故弦AB扫过的面积=π×5² - π×3²=16π.
∵AB//CD,
∴OE⊥AB,
∴AE=BE=$\frac{1}{2}$AB=4.设OE=x,则OF=x + 1.在
Rt△AEO中,OA²=OE²+AE²=x²+4²,
在Rt△DFO中,OD²=OF²+DF²=(x + 1)²+3².
∵OA=OD,
∴x²+4²=(x + 1)²+3²,解得x=3,
∴OD=OA=$\sqrt{3^{2}+4^{2}}$=5,即⊙O的半径为5.
(2)将弦AB绕着圆心O旋转一周,得到的图形是以点O为圆心,3为半径的圆与以点O为圆心,5为半径的圆所围成的圆环,故弦AB扫过的面积=π×5² - π×3²=16π.
查看更多完整答案,请扫码查看


