第46页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10. 如图,在$△ABC$中,$∠ABC= 90^{\circ }$,点$E在CB$的延长线上,$BE= \frac {1}{3}AB$,过点$E作ED⊥AC于点D$.若$AD= ED,AC= 6$,则$CD$的长为(
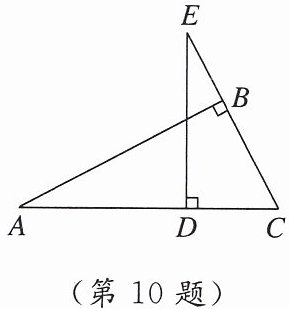
A.1.5
B.2
C.2.5
D.4
B
)
A.1.5
B.2
C.2.5
D.4
答案:
B
11. 母题 教材P133作业题T4 如图,$\odot O是△ABC$的外接圆,$D是\overset{\frown }{AC}$的中点,连结$AD,BD$,其中$BD与AC交于点E$.写出图中所有与$△ADE$相似的三角形:
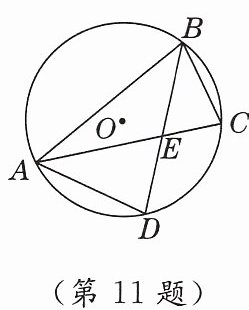
△CBE,△BDA
.
答案:
△CBE,△BDA
12. 如图,在矩形$ABCD$中,$E是BC$的中点,$DF⊥AE$,垂足为$F$.
(1)求证:$△ABE\backsim △DFA$.
(2)若$AB= 6,BC= 4$,求$DF$的长.
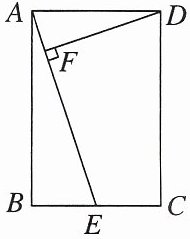
(1)求证:$△ABE\backsim △DFA$.
(2)若$AB= 6,BC= 4$,求$DF$的长.

答案:
(1)[证明]
∵四边形ABCD是矩形,
∴AD//BC,∠BAD=∠B=90°.
∴∠BAE+∠AEB=90°,∠BAE+∠DAF=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=90°=∠B.
∴△ABE∽△DFA.
(2)[解]
∵E是BC的中点,BC=4,
∴BE=2.
∵AB=6,
∴AE=$\sqrt{AB^2+BE^2}$=$\sqrt{6^2+2^2}$=2$\sqrt{10}$.
∵四边形ABCD是矩形,
∴AD=BC=4.
由
(1)得△ABE∽△DFA,
∴$\frac{AB}{DF}$=$\frac{AE}{AD}$.
∴DF=$\frac{AB·AD}{AE}$=$\frac{6×4}{2\sqrt{10}}$=$\frac{6}{5}\sqrt{10}$.
(1)[证明]
∵四边形ABCD是矩形,
∴AD//BC,∠BAD=∠B=90°.
∴∠BAE+∠AEB=90°,∠BAE+∠DAF=90°,
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=90°=∠B.
∴△ABE∽△DFA.
(2)[解]
∵E是BC的中点,BC=4,
∴BE=2.
∵AB=6,
∴AE=$\sqrt{AB^2+BE^2}$=$\sqrt{6^2+2^2}$=2$\sqrt{10}$.
∵四边形ABCD是矩形,
∴AD=BC=4.
由
(1)得△ABE∽△DFA,
∴$\frac{AB}{DF}$=$\frac{AE}{AD}$.
∴DF=$\frac{AB·AD}{AE}$=$\frac{6×4}{2\sqrt{10}}$=$\frac{6}{5}\sqrt{10}$.
13. 新考法 方程思想 如图,在边长为1的正方形$ABCD$中,点$E在边AD$上(不与点$A,D$重合),射线$BE与射线CD交于点F$.
(1)若$ED= \frac {1}{3}$,求$DF$的长;
(2)求证:$AE\cdot CF= 1;$
(3)以点$B$为圆心,$BC$长为半径画弧,交线段$BE于点G$.若$EG= ED$,求$ED$的长.
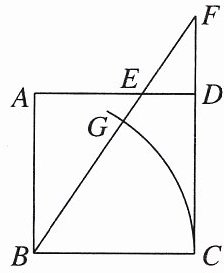
(1)若$ED= \frac {1}{3}$,求$DF$的长;
(2)求证:$AE\cdot CF= 1;$
(3)以点$B$为圆心,$BC$长为半径画弧,交线段$BE于点G$.若$EG= ED$,求$ED$的长.

答案:
(1)[解]
∵ED=$\frac{1}{3}$,正方形ABCD的边长为1,
∴AB=AD=BC=1,AE=AD - ED=$\frac{2}{3}$.
由题意得AB//FC,
∴∠ABE=∠F.又
∵∠AEB=∠DEF,
∴△ABE∽△DFE.
∴$\frac{AB}{DF}$=$\frac{AE}{DE}$=2.
∴DF=$\frac{1}{2}$.
(2)[证明]由题意得AD//BC,
∴∠AEB=∠CBF,
又
∵∠BAE=∠FCB,
∴△ABE∽△CFB.
∴$\frac{AE}{CB}$=$\frac{AB}{CF}$.
又
∵AB=BC=1,
∴AE·CF=AB·BC=1.
(3)[解]由题意得BG=BC=1.设EG=ED=x,得AE=1 - x,BE=1 + x.
在Rt△ABE中,由勾股定理得(1 - x)²+1²=(1 + x)²,
解得x=$\frac{1}{4}$.
∴ED=$\frac{1}{4}$.
(1)[解]
∵ED=$\frac{1}{3}$,正方形ABCD的边长为1,
∴AB=AD=BC=1,AE=AD - ED=$\frac{2}{3}$.
由题意得AB//FC,
∴∠ABE=∠F.又
∵∠AEB=∠DEF,
∴△ABE∽△DFE.
∴$\frac{AB}{DF}$=$\frac{AE}{DE}$=2.
∴DF=$\frac{1}{2}$.
(2)[证明]由题意得AD//BC,
∴∠AEB=∠CBF,
又
∵∠BAE=∠FCB,
∴△ABE∽△CFB.
∴$\frac{AE}{CB}$=$\frac{AB}{CF}$.
又
∵AB=BC=1,
∴AE·CF=AB·BC=1.
(3)[解]由题意得BG=BC=1.设EG=ED=x,得AE=1 - x,BE=1 + x.
在Rt△ABE中,由勾股定理得(1 - x)²+1²=(1 + x)²,
解得x=$\frac{1}{4}$.
∴ED=$\frac{1}{4}$.
14. [2025杭州月考]如图,矩形$ABCD$中,$BC<2AB$,$M是BC$的中点,连结$AM$.将$△ABM沿着AM折叠后得△APM$,延长$AP交CD于点E$,连结$ME$.
(1)求证:$ME平分∠PMC$;
(2)求证:$△EMC\backsim △MAB$.
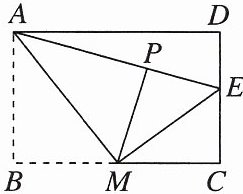
(1)求证:$ME平分∠PMC$;
(2)求证:$△EMC\backsim △MAB$.

答案:
[证明]
(1)
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵M是BC的中点,
∴BM=CM.
∵将△ABM沿着AM折叠后得△APM,
∴PM=BM,∠MPE=∠APM=∠B=90°.
∴PM=CM,∠MPE=∠C.
又
∵EM=EM,
∴△PEM≌△CEM.
∴∠CME=∠PME.
∴ME平分∠PMC.
(2)由折叠可得∠AMB=∠APM,
由
(1)得∠CME=∠PME.
∵∠AMB+∠APM+∠PME+∠CME=180°,
∴∠AMB+∠CME=90°.
∵∠B=90°,
∴∠BAM+∠AMB=90°.
∴∠BAM=∠CME.
又
∵∠B=∠C=90°,
∴△EMC∽△MAB.
(1)
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵M是BC的中点,
∴BM=CM.
∵将△ABM沿着AM折叠后得△APM,
∴PM=BM,∠MPE=∠APM=∠B=90°.
∴PM=CM,∠MPE=∠C.
又
∵EM=EM,
∴△PEM≌△CEM.
∴∠CME=∠PME.
∴ME平分∠PMC.
(2)由折叠可得∠AMB=∠APM,
由
(1)得∠CME=∠PME.
∵∠AMB+∠APM+∠PME+∠CME=180°,
∴∠AMB+∠CME=90°.
∵∠B=90°,
∴∠BAM+∠AMB=90°.
∴∠BAM=∠CME.
又
∵∠B=∠C=90°,
∴△EMC∽△MAB.
查看更多完整答案,请扫码查看


