《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

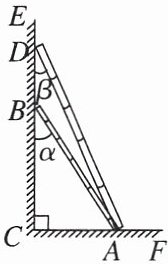
9. 如图,两根竹竿 $ AB $ 和 $ AD $ 斜靠在墙 $ CE $ 上,量得 $ \angle ABC = \alpha $, $ \angle ADC = \beta $,则竹竿 $ AB $ 与 $ AD $ 的长度之比为 (D)

A.$ \frac{\tan \alpha}{\tan \beta} $
B.$ \frac{\cos \alpha}{\cos \beta} $
C.$ \frac{\sin \alpha}{\sin \beta} $
D.$ \frac{\sin \beta}{\sin \alpha} $

答案： D 【点拨】根据题意可知$\angle DCA=90^{\circ },\angle ABC=\alpha ,$$\angle ADC=\beta ,$在$Rt\triangle ABC$中,$\sin \alpha =\frac {AC}{AB}$,即$AC=AB\cdot \sin \alpha ,$在$Rt\triangle ADC$中,$\sin \beta =\frac {AC}{AD}$,即$AC=AD\cdot \sin \beta ,$$\therefore AB\cdot \sin \alpha =AD\cdot \sin \beta ,\therefore \frac {AB}{AD}=\frac {\sin \beta }{\sin \alpha }.$

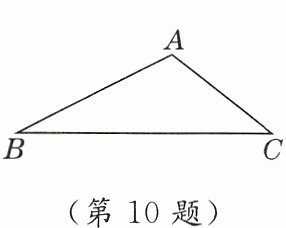
10. 新考法 化斜为直法 如图,在 $ \triangle ABC $ 中, $ \sin B = \frac{\sqrt{5}}{5} $, $ \tan C = \frac{3}{4} $, $ AC = 5 \sqrt{2} $,则 $ BC = $______$10\sqrt{2}$.

答案： $10\sqrt {2}$ 【点拨】过点 A 作$AD⊥BC$于点 D.在$Rt\triangle ACD$中,$\because \tan C=\frac {3}{4},AC=5\sqrt {2},$$\therefore$易得$AD=3\sqrt {2},CD=4\sqrt {2}.$在$Rt\triangle ABD$中,$\because \sin B=\frac {\sqrt {5}}{5},$$\therefore AB=\frac {AD}{\sin B}=\frac {3\sqrt {2}}{\frac {\sqrt {5}}{5}}=3\sqrt {10}.$$\therefore BD=\sqrt {AB^{2}-AD^{2}}=\sqrt {(3\sqrt {10})^{2}-(3\sqrt {2})^{2}}=6\sqrt {2}.$$\therefore BC=BD+CD=6\sqrt {2}+4\sqrt {2}=10\sqrt {2}.$

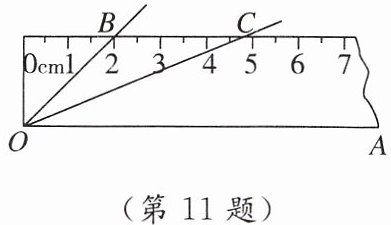
11. [2025 杭州西湖区月考] 如图,将 $ 45^\circ $ 的 $ \angle AOB $ 按下面的方式放置在一把刻度尺上：顶点 $ O $ 与尺下沿的端点重合, $ OA $ 与尺下沿重合, $ OB $ 与尺上沿的交点 $ B $ 在尺上的读数恰为 $ 2 cm $,若按相同的方式将 $ 22.5^\circ $ 的 $ \angle AOC $ 放置在该刻度尺上,则 $ OC $ 与尺上沿的交点 $ C $ 在尺上的读数为______ $ cm $.

答案：
$(2\sqrt {2}+2)$ 【点拨】如图,由题意,得$BC// OA,\angle BDO=90^{\circ },DB=2cm,$$\therefore \angle DBO=\angle AOB=45^{\circ },$$\therefore OB=\frac {BD}{\cos \angle DBO}=2\sqrt {2}cm.$$\because \angle AOC=22.5^{\circ },$$\therefore \angle BOC=\angle AOB-\angle AOC=22.5^{\circ },\angle BCO=\angle AOC=22.5^{\circ },\therefore \angle BOC=\angle BCO,$$\therefore BC=BO=2\sqrt {2}cm,\therefore CD=BC+BD=(2\sqrt {2}+2)cm,$$\therefore OC$与尺上沿的交点 C 在尺上的读数为$(2\sqrt {2}+2)cm.$

12. 如图,在 $ \triangle ABC $ 中, $ AD \perp BC $, $ AE $ 是 $ BC $ 边上的中线, $ AB = 10 $, $ AD = 6 $, $ \tan \angle ACB = 1 $.
(1)求 $ BC $ 的长；
(2)求 $ \sin \angle DAE $ 的值.

答案：
(1)$\because AD⊥BC,AB=10,AD=6,$$\therefore BD=\sqrt {AB^{2}-AD^{2}}=\sqrt {10^{2}-6^{2}}=8.$$\because \tan \angle ACB=\frac {AD}{CD}=1,\therefore CD=AD=6.$$\therefore BC=BD+CD=8+6=14.$
(2)$\because AE$是 BC 边上的中线,$\therefore CE=\frac {1}{2}BC=7.$$\therefore DE=CE-CD=7-6=1.$$\because AD⊥BC,$$\therefore AE=\sqrt {AD^{2}+DE^{2}}=\sqrt {6^{2}+1^{2}}=\sqrt {37}.$$\therefore \sin \angle DAE=\frac {DE}{AE}=\frac {1}{\sqrt {37}}=\frac {\sqrt {37}}{37}.$

13. 如图,在四边形 $ ABCD $ 中,对角线 $ AC $, $ BD $ 交于点 $ E $, $ \angle BAC = 90^\circ $, $ \angle CED = 45^\circ $, $ \angle DCE = 30^\circ $, $ DE = \sqrt{2} $, $ BE = 2 \sqrt{2} $. 求 $ CD $ 的长和四边形 $ ABCD $ 的面积.

答案：
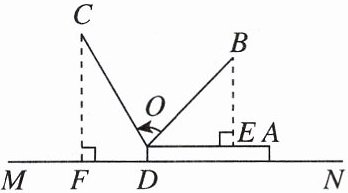
【解】如图,过点 D 作$DH⊥AC$于点 H.$\because \angle CED=45^{\circ },DH⊥EC,$$DE=\sqrt {2},$$\therefore EH=DE\cdot \cos45^{\circ }=\sqrt {2}× \frac {\sqrt {2}}{2}=1,DH=DE\cdot \sin45^{\circ }=\sqrt {2}× \frac {\sqrt {2}}{2}=1.$又$\because \angle DCE=30^{\circ },\therefore HC=\frac {DH}{\tan30^{\circ }}=\sqrt {3},CD=2.$$\because \angle AEB=\angle CED=45^{\circ },\angle BAC=90^{\circ },BE=2\sqrt {2},$$\therefore$易得$AB=AE=2.$$\therefore AC=AE+EH+HC=2+1+\sqrt {3}=3+\sqrt {3}.$$\therefore S_{四边形ABCD}=\frac {1}{2}× 2× (3+\sqrt {3})+\frac {1}{2}× 1× (3+\sqrt {3})=\frac {3\sqrt {3}+9}{2}.$

14. 情境题 生活应用 一本厚度为 $ 2 cm $ 的字典,封面是硬的,翻开时不会发生弯曲. 如图,把这本字典放在桌面 $ MN $ 上,当将上面的封面 $ OA $ 打开 $ 45^\circ $ 角到 $ OB $ 位置时,点 $ B $ 到 $ OA $ 的距离 $ BE = 8 \sqrt{2} cm $. 现将封面 $ OA $ 打开 $ 120^\circ $ 角到 $ OC $ 位置,请回答下列问题(计算时不考虑封面的厚度).
(1)求字典的封面宽 $ OB $ 的长度；
(2)求点 $ C $ 到桌面 $ MN $ 的距离 $ CF $.

答案：

(1)依题意得$\angle BOE=45^{\circ },BE=8\sqrt {2}cm,\angle BEO=90^{\circ },\therefore OB=\frac {BE}{\sin \angle BOE}=\frac {8\sqrt {2}}{\sin45^{\circ }}=16(cm).(2)$延长 EO 交 CF 于点 H,如图所示.依题意得$\angle EOC=120^{\circ },OC=OB=16cm,\angle CFD=90^{\circ },OE// MN,\therefore HF=OD=2cm,\angle CHO=90^{\circ },\angle COH=180^{\circ }-\angle EOC=60^{\circ }.$在$Rt\triangle OCH$中$,\sin \angle COH=\frac {CH}{CO},\therefore CH=CO\cdot \sin \angle COH=16×\sin60^{\circ }=8\sqrt {3}(cm).$$\therefore CF=CH+HF=(8\sqrt {3}+2)cm.$