第26页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 垂径定理:垂直于弦的直径平分
这条弦
,并且平分弦所对的弧
。
答案:
这条弦;弦所对的弧
1. 如图,在$\odot O$中,直径$CD垂直弦AB于点E$,则下列结论错误的是(

A.$AE = BE$
B.$EO = ED$
C.$\overset{\frown}{AD} = \overset{\frown}{BD}$
D.$\overset{\frown}{AC} = \overset{\frown}{BC}$
B
)
A.$AE = BE$
B.$EO = ED$
C.$\overset{\frown}{AD} = \overset{\frown}{BD}$
D.$\overset{\frown}{AC} = \overset{\frown}{BC}$
答案:
B
2. [2025宁波第七中学月考]如图,$\odot O的直径CD垂直弦AB于点E$,且$OE = 1\ cm$,$DE = 4\ cm$,则$AB$的长为(
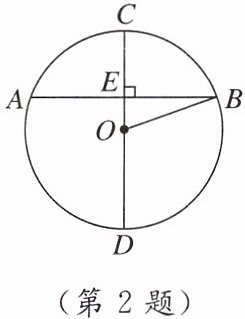
A.$\sqrt{10}\ cm$
B.$2\sqrt{10}\ cm$
C.$2\sqrt{2}\ cm$
D.$4\sqrt{2}\ cm$
D
)
A.$\sqrt{10}\ cm$
B.$2\sqrt{10}\ cm$
C.$2\sqrt{2}\ cm$
D.$4\sqrt{2}\ cm$
答案:
D
3. 如图所示为小佳同学用直尺和圆规作$\overset{\frown}{AB}$的中点的示意图,若图中$AB = 4\ cm$,$EF = 1\ cm$,则$\overset{\frown}{AB}$所在圆的半径是(

A.$\sqrt{3}\ cm$
B.$\sqrt{5}\ cm$
C.$\dfrac{5}{2}\ cm$
D.$5\ cm$
C
)
A.$\sqrt{3}\ cm$
B.$\sqrt{5}\ cm$
C.$\dfrac{5}{2}\ cm$
D.$5\ cm$
答案:
C
4. 如图,$\odot O的半径为5$,若$OP = 3$,则经过点$P$的弦的长可能是(
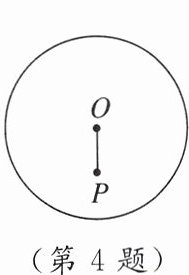
A.$3$
B.$6$
C.$9$
D.$12$
C
) 
A.$3$
B.$6$
C.$9$
D.$12$
答案:
C
5. [2025杭州绿城育华学校月考]如图,$\odot O的半径为5$,$M$是圆外一点,$MO = 6$,$\angle OMA = 30^{\circ}$,则弦$AB$的长为____

8
。
答案:
8
6. 如图,$O的直径为20$,弦$AB的长为12$,$P是弦AB$上一点,则线段$OP$长度的最小值为
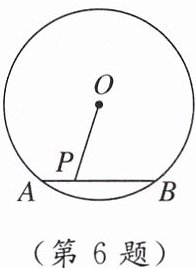
8
。
答案:
8
7. 温州有很多历史悠久的石拱桥,它们是圆弧形的桥梁,如图是温州某地的石拱桥局部示意图,其跨度$AB为24$米,拱高$CD为4$米,则这个弧形石拱桥设计的半径为

20
米。
答案:
20
8. 如图,一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图(单位:$cm$),则液面宽度$AB = $
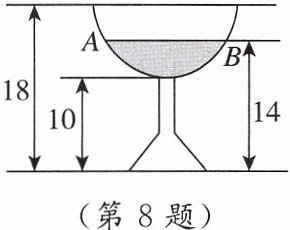
$8\sqrt{3}$
$cm$。
答案:
$8\sqrt{3}$
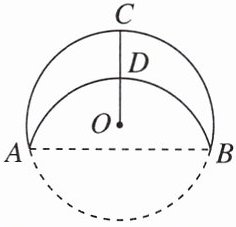
9. [2025杭州中学月考]如图,将半径为$8的\odot O沿AB$折叠,$\overset{\frown}{AB}恰好经过与AB垂直的半径OC的中点D$,则折痕$AB$长为(
A.$4\sqrt{10}$
B.$4\sqrt{15}$
C.$12$
D.$8\sqrt{3}$
B
)
A.$4\sqrt{10}$
B.$4\sqrt{15}$
C.$12$
D.$8\sqrt{3}$
答案:
B
10. 新考法分类讨论法已知在$\odot O中两条平行弦AB// CD$,$AB = 12$,$CD = 16$,$\odot O的半径是10$,则$AB与CD$间的距离是(
A.$6或12$
B.$2或14$
C.$6或14$
D.$2或12$
B
)A.$6或12$
B.$2或14$
C.$6或14$
D.$2或12$
答案:
B 【点拨】①当AB和CD位于圆心同侧时,如图,连结OA,OC,过点O作OE⊥AB于点E,交CD于点F,则$AE=\frac{1}{2}AB=6$.
∵AB//CD,
∴OE⊥CD,
∴$CF=\frac{1}{2}CD=8$.
∵OA=OC=10,
∴$OE=\sqrt{OA^2 - AE^2}=8$,$OF=\sqrt{OC^2 - CF^2}=6$,
∴EF=OE - OF=2,即此时AB与CD间的距离是2;②当AB和CD位于圆心异侧时,如图,连结OA,OC,过点O作OP⊥AB于点P,延长PO交CD于点Q,则$AP=\frac{1}{2}AB=6$.
∵AB//CD,
∴OQ⊥CD,
∴$CQ=\frac{1}{2}CD=8$.
∵OA=OC=10,
∴$OP=\sqrt{OA^2 - AP^2}=8$,$OQ=\sqrt{OC^2 - CQ^2}=6$,
∴PQ=OP + OQ=14,即此时AB与CD间的距离是14.综上可知,AB与CD间的距离是2或14.
∵AB//CD,
∴OE⊥CD,
∴$CF=\frac{1}{2}CD=8$.
∵OA=OC=10,
∴$OE=\sqrt{OA^2 - AE^2}=8$,$OF=\sqrt{OC^2 - CF^2}=6$,
∴EF=OE - OF=2,即此时AB与CD间的距离是2;②当AB和CD位于圆心异侧时,如图,连结OA,OC,过点O作OP⊥AB于点P,延长PO交CD于点Q,则$AP=\frac{1}{2}AB=6$.
∵AB//CD,
∴OQ⊥CD,
∴$CQ=\frac{1}{2}CD=8$.
∵OA=OC=10,
∴$OP=\sqrt{OA^2 - AP^2}=8$,$OQ=\sqrt{OC^2 - CQ^2}=6$,
∴PQ=OP + OQ=14,即此时AB与CD间的距离是14.综上可知,AB与CD间的距离是2或14.
查看更多完整答案,请扫码查看


