《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

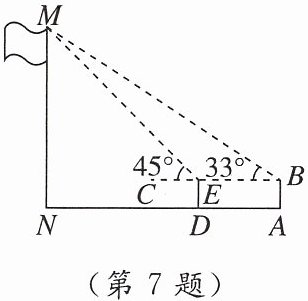
7. 某校数学兴趣小组开展综合实践活动——测量校园内旗杆的高度.如图,已知测倾器AB的高度为1.5米,在测点A处安置测倾器,测得旗杆顶部点M的仰角∠MBC= 33°,在与点A相距4.5米的点D处安置测倾器,测得点M的仰角∠MEC= 45°(点A,D,N在同一条水平线上,且点M,N,D,A,B,E,C都在同一竖直平面内,点B,E,C在同一直线上),则旗杆顶部离地面的高度MN为9.9米.(精确到0.1米,参考数据：sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)

答案： 9.9米

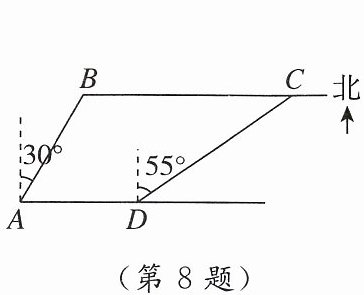
8. 如图,小亮为测量某铁桥的长度,乘车在与该铁桥平行且处于同一水平面的一段东西走向的公路上行驶时,在A处发现桥的起点B在A点的北偏东30°的方向上,并测得AB= 160米,当车前进146米到达D处时,测得桥的终点C在D点的北偏东55°的方向上,则该桥的长度BC约为264米.(结果保留整数,参考数据：sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,$\sqrt{3}$≈1.73)

答案： 264米

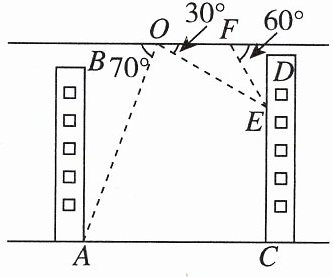
9. [2025绍兴模拟]某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案：如图,无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为66m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24m到达点F,测得点E处的俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.(参考数据：sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,$\sqrt{3}$≈1.73)
(1)求EF的长；
(2)求楼AB与CD之间的距离AC的长.

答案：
(1)由题意得$OF=24m$.如图.$\because ∠FOE=30^{\circ },$$∠PFE=60^{\circ },$
$\therefore ∠FEO=60^{\circ }-30^{\circ }=30^{\circ }=∠FOE,$
$\therefore EF=OF=24m.$
(2)延长AB,CD分别与直线OF交于点G和H,如图.
易知$AC=GH.$
在Rt△AGO中,$∠AOG=70^{\circ },$
$\therefore OG=\frac {AG}{\tan 70^{\circ }}\approx \frac {66}{2.75}=24(m).$
在Rt△EFH中,$∠HFE=60^{\circ },$
$\therefore FH=EF\cdot \cos 60^{\circ }=24×\frac {1}{2}=12(m),$
$\therefore AC=GH=OG+OF+FH\approx 24+24+12=60(m),$
$\therefore$楼AB与CD之间的距离AC的长约为60m.

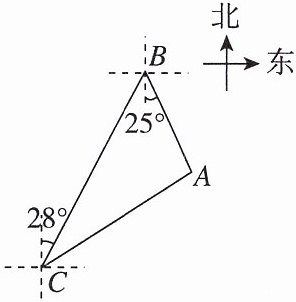
10. [2025杭州月考]在某海域开展的“海上联合”反潜演习中,我方军舰要到达C岛完成任务.如图,已知军舰位于B市的南偏东25°方向上的A处,且在C岛的北偏东58°方向上,B市在C岛的北偏东28°方向上,且距离C岛372km,此时,我方军舰沿着AC方向以30km/h的速度航行.(参考数据：$\sqrt{3}\approx1.73$,sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$)
(1)求出∠ABC和∠ACB的大小.
(2)我方军舰大约需要多长时间到达C岛?

答案：
(1)
∵A处在C岛的北偏东58°方向上,B市在C岛的北偏东28°方向上,
$\therefore ∠ACB=58^{\circ }-28^{\circ }=30^{\circ },$C岛在B市的南偏西28°方向上.
又
∵A处位于B市的南偏东25°方向上,
$\therefore ∠ABC=28^{\circ }+25^{\circ }=53^{\circ }.$
(2)过点A作$AD⊥BC$于点D,设$AD=xkm.$
在Rt△ABD中,$\because ∠ABD=53^{\circ },$
$\therefore BD=\frac {AD}{\tan 53^{\circ }}\approx \frac {3}{4}xkm.$
在Rt△ACD中,$\because ∠ACD=30^{\circ },$
$\therefore CD=\frac {AD}{\tan 30^{\circ }}=\sqrt {3}xkm.$
$\because BD+CD=BC,BC=372km,$
$\therefore \frac {3}{4}x+\sqrt {3}x\approx 372$,解得$x\approx 150,\therefore AD\approx 150km.$
$\because ∠ACD=30^{\circ },∠ADC=90^{\circ },\therefore AC=2AD\approx 300km,$$300÷30=10(h).$
答:我方军舰大约需要10h到达C岛.