第57页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. $\triangle ABC的三边长分别为2$,$3$,$4$,另有一个与它相似的三角形$DEF$,其最长边长为$12$,则$\triangle DEF$的周长是(
A.$54$
B.$36$
C.$27$
D.$21$
C
)A.$54$
B.$36$
C.$27$
D.$21$
答案:
C
10. 如图,在矩形$ABCD$中,$AB = 8$,$AD = 16$,$E是AC$上的点,且$CE = 2AE$,连结$DE$并延长,交$AB于点F$,作$CG\perp DF$,分别交$AD$,$DF于点G$,$H$,则$DG$的长为(
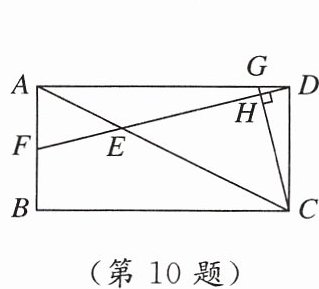
A.$1$
B.$2$
C.$3$
D.$4$
B
)
A.$1$
B.$2$
C.$3$
D.$4$
答案:
B [点拨]
∵四边形ABCD是矩形,AB=8,AD=16,
∴AB//CD,AB=CD=8,AD=BC=16,∠DAF=∠ADC=∠ADF+∠CDH=90°.
∴易得△AEF∽△CED,
∴$\frac{AE}{CE}=\frac{AF}{CD}$.
∵CE=2AE,
∴$\frac{AF}{8}=\frac{1}{2}$.
∴AF=4.
∵CG⊥DF,
∴∠CDH+∠DCG=90°.
∴∠ADF=∠DCG.
∵∠DAF=∠CDG=90°,
∴△DAF∽△CDG.
∴$\frac{AD}{CD}=\frac{AF}{DG}$,即$\frac{16}{8}=\frac{4}{DG}$.
∴DG=2.
∵四边形ABCD是矩形,AB=8,AD=16,
∴AB//CD,AB=CD=8,AD=BC=16,∠DAF=∠ADC=∠ADF+∠CDH=90°.
∴易得△AEF∽△CED,
∴$\frac{AE}{CE}=\frac{AF}{CD}$.
∵CE=2AE,
∴$\frac{AF}{8}=\frac{1}{2}$.
∴AF=4.
∵CG⊥DF,
∴∠CDH+∠DCG=90°.
∴∠ADF=∠DCG.
∵∠DAF=∠CDG=90°,
∴△DAF∽△CDG.
∴$\frac{AD}{CD}=\frac{AF}{DG}$,即$\frac{16}{8}=\frac{4}{DG}$.
∴DG=2.
11. 如图,在$\triangle ABC$中,点$E是AB$边上的点,点$F是AC$边上的点,且$EF// BC$,$AE:EB = 3:1$,点$D是AE$的中点,若$\triangle ABC的面积为32$,则$\triangle DEF$的面积为(

A.$18$
B.$12$
C.$10$
D.$9$
D
)
A.$18$
B.$12$
C.$10$
D.$9$
答案:
D [点拨]
∵AE:BE=3:1,
∴AE:AB=3:4.
∵EF//BC,
∴△AEF∽△ABC;
∴$\frac{S_{\triangle AEF}}{S_{\triangle ABC}}=(\frac{AE}{AB})^2=(\frac{3}{4})^2=\frac{9}{16}$.
∵S△ABC=32,
∴S△AEF=18.
∵D是AE的中点,
∴S△DEF=$\frac{1}{2}S_{\triangle AEF}=9$.
∵AE:BE=3:1,
∴AE:AB=3:4.
∵EF//BC,
∴△AEF∽△ABC;
∴$\frac{S_{\triangle AEF}}{S_{\triangle ABC}}=(\frac{AE}{AB})^2=(\frac{3}{4})^2=\frac{9}{16}$.
∵S△ABC=32,
∴S△AEF=18.
∵D是AE的中点,
∴S△DEF=$\frac{1}{2}S_{\triangle AEF}=9$.
12. 如图,已知矩形$ABCD$,点$E在CB$延长线上,点$F在BC$延长线上,过点$F作FH\perp EF交ED的延长线于点H$,连结$AF交EH于点G$,$GE = GH$.
(1)求证:$BE = CF$;
(2)当$\frac{AB}{FH}= \frac{5}{6}$,$AD = 4$时,求$EF$的长.
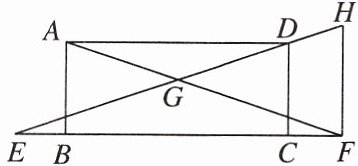
(1)求证:$BE = CF$;
(2)当$\frac{AB}{FH}= \frac{5}{6}$,$AD = 4$时,求$EF$的长.

答案:
(1)[证明]
∵FH⊥EF,GE=GH,
∴GE=GF=GH.
∴∠GFE=∠E.
∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°.
∴△ABF≌△DCE(AAS).
∴BF=CE;
∴BF−BC=CE−BC,即CF=BE.
(2)[解]易知CD//FH,
∴△DCE∽△HFE.
∴$\frac{EC}{EF}=\frac{CD}{FH}$.
∵CD=AB,
∴$\frac{CD}{FH}=\frac{AB}{FH}=\frac{5}{6}$.
∴$\frac{CE}{EF}=\frac{5}{6}$. 易知BC=AD=4,设BE=CF=x, 则CE=x+4,EF=2x+4,
∴$\frac{CE}{EF}=\frac{x+4}{2x+4}=\frac{5}{6}$,解得x=1,
∴EF=6.
(1)[证明]
∵FH⊥EF,GE=GH,
∴GE=GF=GH.
∴∠GFE=∠E.
∵四边形ABCD是矩形,
∴AB=CD,∠ABC=∠DCB=90°.
∴△ABF≌△DCE(AAS).
∴BF=CE;
∴BF−BC=CE−BC,即CF=BE.
(2)[解]易知CD//FH,
∴△DCE∽△HFE.
∴$\frac{EC}{EF}=\frac{CD}{FH}$.
∵CD=AB,
∴$\frac{CD}{FH}=\frac{AB}{FH}=\frac{5}{6}$.
∴$\frac{CE}{EF}=\frac{5}{6}$. 易知BC=AD=4,设BE=CF=x, 则CE=x+4,EF=2x+4,
∴$\frac{CE}{EF}=\frac{x+4}{2x+4}=\frac{5}{6}$,解得x=1,
∴EF=6.
13. $\triangle CAB和\triangle CDE$都是直角三角形,$\angle ACB = \angle DCE = 90^{\circ}$,$CB = mCA$,$CE = mCD$,连结$AD$,$BE$,探究$AD$,$BE$的位置关系.
(1)如图①,当$m = 1$时,直接写出$AD$,$BE$的位置关系:
(2)如图②,当$m\neq1$时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.
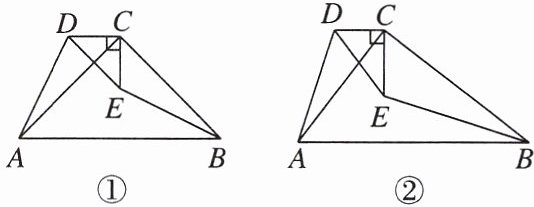
(1)如图①,当$m = 1$时,直接写出$AD$,$BE$的位置关系:
BE⊥AD
.(2)如图②,当$m\neq1$时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.

(2)成立.证明如下: 延长BE交AD于点G.
∵∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠ACE+∠ECB=90°.
∴∠DCA=∠ECB.
∵$\frac{DC}{CE}=\frac{AC}{BC}=\frac{1}{m}$,
∴△DCA∽△ECB.
∴∠DAC=∠CBE.
∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°−∠ACB=90°,
∴∠AGB=180°−90°=90°.
∴BE⊥AD.
∵∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠ACE+∠ECB=90°.
∴∠DCA=∠ECB.
∵$\frac{DC}{CE}=\frac{AC}{BC}=\frac{1}{m}$,
∴△DCA∽△ECB.
∴∠DAC=∠CBE.
∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°−∠ACB=90°,
∴∠AGB=180°−90°=90°.
∴BE⊥AD.
答案:
(1)BE⊥AD
(2)成立.证明如下: 延长BE交AD于点G.
∵∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠ACE+∠ECB=90°.
∴∠DCA=∠ECB.
∵$\frac{DC}{CE}=\frac{AC}{BC}=\frac{1}{m}$,
∴△DCA∽△ECB.
∴∠DAC=∠CBE.
∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°−∠ACB=90°,
∴∠AGB=180°−90°=90°.
∴BE⊥AD.
(1)BE⊥AD
(2)成立.证明如下: 延长BE交AD于点G.
∵∠DCE=∠ACB=90°,
∴∠DCA+∠ACE=∠ACE+∠ECB=90°.
∴∠DCA=∠ECB.
∵$\frac{DC}{CE}=\frac{AC}{BC}=\frac{1}{m}$,
∴△DCA∽△ECB.
∴∠DAC=∠CBE.
∵∠GAB+∠ABG=∠DAC+∠CAB+∠ABG=∠CBE+∠CAB+∠ABG=∠CAB+∠CBA=180°−∠ACB=90°,
∴∠AGB=180°−90°=90°.
∴BE⊥AD.
14. 新考向 数学文化 《周髀算经》中记载了“偃矩以望高”的方法.“矩”在古代指两条边呈直角的曲尺(即图中的$ABC$).“偃矩以望高”的意思是把“矩”仰立放,可测量物体的高度. 如图,点$A$,$B$,$Q$在同一水平线上,$\angle ABC和\angle AQP$均为直角,$AP与BC相交于点D$. 测得$AB = 40cm$,$BD = 20cm$,$AQ = 12m$,则树高$PQ = $____

6
$m$.
答案:
6
查看更多完整答案,请扫码查看


