第60页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10. [2025 丽水模拟]如图,在$Rt△ABC$中,$∠ACB= 90^{\circ }$,$BC= 5$,$AC= 12$,$CD⊥AB于D$.求:(1)$sinA$的值;(2)$cos∠ACD$的值;(3)$CD$的值.
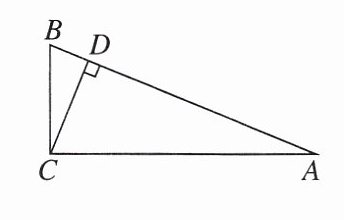

答案:
[解]
(1)
∵∠ACB=90°,BC=5,AC=12,
∴AB=13.
∴sinA=$\frac{BC}{AB}$=$\frac{5}{13}$.
(2)
∵CD⊥AB于D,∠ACB=90°,
∴∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
∴cos∠ACD=cosB=$\frac{BC}{AB}$=$\frac{5}{13}$.
(3)
∵AC=12,sinA=$\frac{5}{13}$,
∴sinA=$\frac{CD}{AC}$=$\frac{CD}{12}$=$\frac{5}{13}$,
∴CD=$\frac{60}{13}$.
(1)
∵∠ACB=90°,BC=5,AC=12,
∴AB=13.
∴sinA=$\frac{BC}{AB}$=$\frac{5}{13}$.
(2)
∵CD⊥AB于D,∠ACB=90°,
∴∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
∴cos∠ACD=cosB=$\frac{BC}{AB}$=$\frac{5}{13}$.
(3)
∵AC=12,sinA=$\frac{5}{13}$,
∴sinA=$\frac{CD}{AC}$=$\frac{CD}{12}$=$\frac{5}{13}$,
∴CD=$\frac{60}{13}$.
11. 母题·教材 P7 作业题 T7 如图,一根 3m 长的竹竿$AB$斜靠在竖直的墙上,沿着墙下滑,点$A下滑至点A'$,点$B移至点B'$,设$∠ABC= α$,$∠A'B'C= β$,则$AA'= $
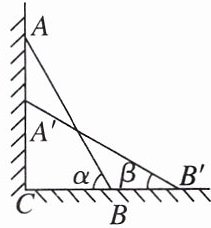
A.$(3sinα - 3sinβ)m$
B.$(3cosα - 3cosβ)m$
C.$(\frac {3}{tanα}-\frac {3}{tanβ})m$
D.$(3tanα - 3tanβ)m$
A
( )
A.$(3sinα - 3sinβ)m$
B.$(3cosα - 3cosβ)m$
C.$(\frac {3}{tanα}-\frac {3}{tanβ})m$
D.$(3tanα - 3tanβ)m$
答案:
A [点拨]在Rt△ABC中,∠ACB=90°,∠ABC=α,则sinα=$\frac{AC}{AB}$,即AC=AB·sinα=3sinαm,同理,A'C=A'B'·sinβ=3sinβm,
∴AA'=AC - A'C=(3sinα - 3sinβ)m.
∴AA'=AC - A'C=(3sinα - 3sinβ)m.
12. 新考向 数学文化 如图为我国古代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.图形是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是 120,小正方形的面积是 20,则$sinθ - cosθ= $______.
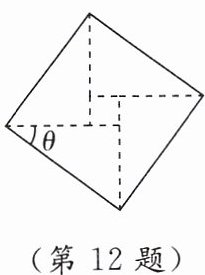

答案:
-$\frac{\sqrt{6}}{6}$ [点拨]如图所示.
∵大正方形的面积是120,小正方形的面积是20,
∴大正方形的边长AB=2$\sqrt{30}$,小正方形的边长CD=2$\sqrt{5}$.
∵AC=BD,
∴sinθ - cosθ=$\frac{BD}{AB}$ - $\frac{AD}{AB}$=-$\frac{AD - BD}{AB}$=-$\frac{CD}{AB}$=-$\frac{2\sqrt{5}}{2\sqrt{30}}$=-$\frac{\sqrt{6}}{6}$.

-$\frac{\sqrt{6}}{6}$ [点拨]如图所示.
∵大正方形的面积是120,小正方形的面积是20,
∴大正方形的边长AB=2$\sqrt{30}$,小正方形的边长CD=2$\sqrt{5}$.
∵AC=BD,
∴sinθ - cosθ=$\frac{BD}{AB}$ - $\frac{AD}{AB}$=-$\frac{AD - BD}{AB}$=-$\frac{CD}{AB}$=-$\frac{2\sqrt{5}}{2\sqrt{30}}$=-$\frac{\sqrt{6}}{6}$.

13. 如图,在$Rt△ABC$中,$∠B= 90^{\circ }$,$AB= 5$,$BC= 12$,将$△ABC绕点A逆时针旋转得到△ADE$,使得点$D落在AC$上,连结$EC$,则$tan∠ECD$的值为______.
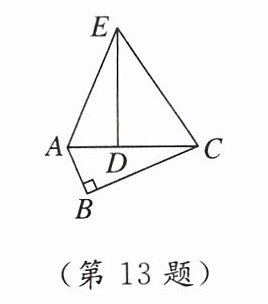

答案:
$\frac{3}{2}$ [点拨]
∵在Rt△ABC中,∠B=90°,AB=5,BC=12,
∴AC=$\sqrt{AB^2 + BC^2}$=13.
由旋转得AD=AB=5,DE=BC=12,∠ADE=∠B=90°,
∴∠CDE=90°,CD=AC - AD=8,
∴tan∠ECD=$\frac{DE}{CD}$=$\frac{12}{8}$=$\frac{3}{2}$.
∵在Rt△ABC中,∠B=90°,AB=5,BC=12,
∴AC=$\sqrt{AB^2 + BC^2}$=13.
由旋转得AD=AB=5,DE=BC=12,∠ADE=∠B=90°,
∴∠CDE=90°,CD=AC - AD=8,
∴tan∠ECD=$\frac{DE}{CD}$=$\frac{12}{8}$=$\frac{3}{2}$.
14. 在$△ABC$中,$∠C= 90^{\circ }$,$a$,$b$,$c分别为∠A$,$∠B$,$∠C$的对边,若$a^{2}= bc$,则$sinB= $
$\frac{\sqrt{5}-1}{2}$
.
答案:
$\frac{\sqrt{5}-1}{2}$ [点拨]
∵a²=bc,
∴b=$\frac{a^2}{c}$,
∴sinB=$\frac{b}{c}$=$\frac{\frac{a^2}{c}}{c}$=$\frac{a^2}{c^2}$=($\frac{a}{c}$)²=sin²A.
∵sinB=$\frac{b}{c}$,
∴sin²B=$\frac{b^2}{c^2}$,
∴sin²A+sin²B=$\frac{a^2 + b^2}{c^2}$=$\frac{c^2}{c^2}$=1.
∴sin²B+sinB - 1=0,
∴sinB=$\frac{\sqrt{5}-1}{2}$(负值已舍去).
∵a²=bc,
∴b=$\frac{a^2}{c}$,
∴sinB=$\frac{b}{c}$=$\frac{\frac{a^2}{c}}{c}$=$\frac{a^2}{c^2}$=($\frac{a}{c}$)²=sin²A.
∵sinB=$\frac{b}{c}$,
∴sin²B=$\frac{b^2}{c^2}$,
∴sin²A+sin²B=$\frac{a^2 + b^2}{c^2}$=$\frac{c^2}{c^2}$=1.
∴sin²B+sinB - 1=0,
∴sinB=$\frac{\sqrt{5}-1}{2}$(负值已舍去).
15. 如图,在$Rt△ABC$中,$∠C= 90^{\circ }$,$a$,$b$,$c分别表示Rt△ABC中∠A$,$∠B$,$∠C$的对边.
(1)$sinA= $
(2)观察(1)的计算结果,你能发现$sinA与cosB$,$tanA与tanB$之间有什么关系吗?
(3)①若$sinA= \frac {2}{3}$,则$cosB= $
②若$tanA= 2$,则$tanB= $
(4)若$sin^{2}A表示(sinA)^{2}$,$cos^{2}A表示(cosA)^{2}$,求证:$sin^{2}A+cos^{2}A= 1$.
(1)$sinA= $
$\frac{a}{c}$
,$cosB= $$\frac{a}{c}$
,$tanA= $$\frac{a}{b}$
,$tanB= $$\frac{b}{a}$
;(2)观察(1)的计算结果,你能发现$sinA与cosB$,$tanA与tanB$之间有什么关系吗?
[解]由(1)知sinA=cosB,tanA·tanB=1.
(3)①若$sinA= \frac {2}{3}$,则$cosB= $
$\frac{2}{3}$
;②若$tanA= 2$,则$tanB= $
$\frac{1}{2}$
.(4)若$sin^{2}A表示(sinA)^{2}$,$cos^{2}A表示(cosA)^{2}$,求证:$sin^{2}A+cos^{2}A= 1$.
[证明]∵在Rt△ABC中,∠C=90°,∴a²+b²=c².∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,∴sin²A+cos²A=($\frac{a}{c}$)²+($\frac{b}{c}$)²=$\frac{a^2 + b^2}{c^2}$=1.
答案:
(1)$\frac{a}{c}$;$\frac{a}{c}$;$\frac{a}{b}$;$\frac{b}{a}$
(2)[解]由
(1)知sinA=cosB,tanA·tanB=1.
(3)①$\frac{2}{3}$ ②$\frac{1}{2}$
(4)[证明]
∵在Rt△ABC中,∠C=90°,
∴a²+b²=c².
∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴sin²A+cos²A=($\frac{a}{c}$)²+($\frac{b}{c}$)²=$\frac{a^2 + b^2}{c^2}$=1.
(1)$\frac{a}{c}$;$\frac{a}{c}$;$\frac{a}{b}$;$\frac{b}{a}$
(2)[解]由
(1)知sinA=cosB,tanA·tanB=1.
(3)①$\frac{2}{3}$ ②$\frac{1}{2}$
(4)[证明]
∵在Rt△ABC中,∠C=90°,
∴a²+b²=c².
∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴sin²A+cos²A=($\frac{a}{c}$)²+($\frac{b}{c}$)²=$\frac{a^2 + b^2}{c^2}$=1.
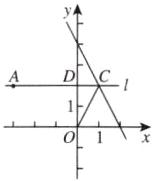
16. 新趋势 学科内综合 在平面直角坐标系$xOy$中,反比例函数$y= \frac {k}{x}$($k为常数且k≠0$)的图象上有一点$A(-3,m)$,且与直线$y= -2x+4交于另一点B(n,6)$.
(1)求$k与m$的值;
(2)过点$A作直线l// x$轴,与直线$y= -2x+4交于点C$,求$sin∠OCA$的值.
(1)求$k与m$的值;
(2)过点$A作直线l// x$轴,与直线$y= -2x+4交于点C$,求$sin∠OCA$的值.

答案:
[解]
(1)把B(n,6)的坐标代入y=-2x+4,得6=-2n+4,解得n=-1,
∴B(-1,6),
把B(-1,6)的坐标代入y=$\frac{k}{x}$,得k=-1×6=-6,
∴y=-$\frac{6}{x}$,
把A(-3,m)的坐标代入y=-$\frac{6}{x}$,得m=-$\frac{6}{-3}$=2.
(2)由
(1)知,A(-3,2),设l与y轴相交于D,如图.
∵l//x轴,x轴⊥y轴,
∴A,C,D三点的纵坐标相同,均为2,∠CDO=90°,
∴OD=2.
把y=2代入y=-2x+4,得2=-2x+4,解得x=1,
∴C(1,2),
∴CD=1,
∴OC=$\sqrt{CD^2 + OD^2}$=$\sqrt{5}$,
∴sin∠OCA=$\frac{OD}{OC}$=$\frac{2\sqrt{5}}{5}$.
[解]
(1)把B(n,6)的坐标代入y=-2x+4,得6=-2n+4,解得n=-1,
∴B(-1,6),
把B(-1,6)的坐标代入y=$\frac{k}{x}$,得k=-1×6=-6,
∴y=-$\frac{6}{x}$,
把A(-3,m)的坐标代入y=-$\frac{6}{x}$,得m=-$\frac{6}{-3}$=2.
(2)由
(1)知,A(-3,2),设l与y轴相交于D,如图.
∵l//x轴,x轴⊥y轴,
∴A,C,D三点的纵坐标相同,均为2,∠CDO=90°,
∴OD=2.
把y=2代入y=-2x+4,得2=-2x+4,解得x=1,
∴C(1,2),
∴CD=1,
∴OC=$\sqrt{CD^2 + OD^2}$=$\sqrt{5}$,

∴sin∠OCA=$\frac{OD}{OC}$=$\frac{2\sqrt{5}}{5}$.
查看更多完整答案,请扫码查看


