第28页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
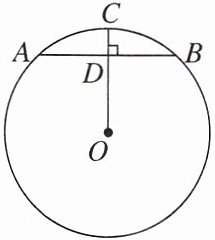
例1 母题 教材P78作业题T2 如图,在$\odot O$中,半径$OC\perp AB于点D$。已知$\odot O$的半径为3,$AB = 4$。求$DC$的长(精确到0.01)。
方法点拨:求圆中的弦长或其他线段长时,通常连半径,由半径、弦的一半以及圆心到弦的距离构成直角三角形进行求解。

方法点拨:求圆中的弦长或其他线段长时,通常连半径,由半径、弦的一半以及圆心到弦的距离构成直角三角形进行求解。
答案:
【解】连结OA.
∵OC⊥AB,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
∴OD=$\sqrt{OA^{2}-AD^{2}}$=$\sqrt{3^{2}-2^{2}}$=$\sqrt{5}$,
∴DC=OC-OD=3-$\sqrt{5}$≈0.76.
∵OC⊥AB,
∴AD=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2,
∴OD=$\sqrt{OA^{2}-AD^{2}}$=$\sqrt{3^{2}-2^{2}}$=$\sqrt{5}$,
∴DC=OC-OD=3-$\sqrt{5}$≈0.76.
变式1-1 如图,$\odot O的直径CD = 10$,$AB是\odot O$的弦,$AB\perp CD$,垂足为$M$,$OM:MC = 3:2$,则$AB$的长为(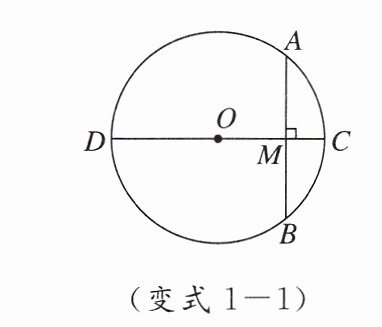
A.$8\sqrt{3}$
B.4
C.16
D.8
D
)
A.$8\sqrt{3}$
B.4
C.16
D.8
答案:
D
变式1-2 如图,在$\odot O$中,弦$AB$的长为2,点$C在AB$上移动,连结$OC$,过点$C作CD\perp OC交\odot O于点D$,则$CD$的最大值为(
A.4
B.2
C.$\sqrt{2}$
D.1
D
)
A.4
B.2
C.$\sqrt{2}$
D.1
答案:
D
例2 母题 教材P78作业题T6 已知:如图,在$\odot O$中,弦$AB// CD$。求证:$\overset{\frown}{AC}= \overset{\frown}{BD}$。

方法点拨:当圆中出现弦时,通常过圆心作弦的垂线,再连半径构造直角三角形,可通过垂径定理或勾股定理解题。

方法点拨:当圆中出现弦时,通常过圆心作弦的垂线,再连半径构造直角三角形,可通过垂径定理或勾股定理解题。
答案:
【证明】过点O作OE⊥AB,交⊙O于点E,
∵AB//CD,
∴OE⊥CD.
∴弧AE=弧EB,弧CE=弧ED.
∴弧CE - 弧AE=弧ED - 弧EB,
即弧AC=弧BD.
∵AB//CD,
∴OE⊥CD.
∴弧AE=弧EB,弧CE=弧ED.
∴弧CE - 弧AE=弧ED - 弧EB,
即弧AC=弧BD.
变式2-1 如图,在半圆$ACB$中,$AB = 6$,将半圆$ACB沿弦BC$所在的直线折叠,若弧$BC恰好过圆心O$,则$BC$的长是(
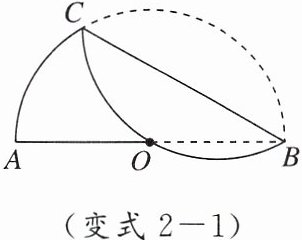
A.$3\sqrt{3}$
B.$2\pi$
C.$3\sqrt{2}$
D.$2\sqrt{6}$
A
)
A.$3\sqrt{3}$
B.$2\pi$
C.$3\sqrt{2}$
D.$2\sqrt{6}$
答案:
A
变式2-2 如图,在$\odot O$中,弦$AB与弦CD交于点P$,且$AB\perp CD$,$DP = 2$,$CP = 6$,$AP = 4$,则$\odot O$的半径为(
A.$\sqrt{65}$
B.4
C.$\frac{\sqrt{65}}{2}$
D.5
C
)
A.$\sqrt{65}$
B.4
C.$\frac{\sqrt{65}}{2}$
D.5
答案:
C
查看更多完整答案,请扫码查看


