第36页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
扇形面积公式:如果扇形的半径为R,圆心角为$n^{\circ}$,扇形的弧长为l,那么扇形的面积$S= $______$=$______.
答案:
$\frac{n\pi R^{2}}{360}$;$\frac{1}{2}lR$
1. 母题 教材P107作业题T1 已知扇形的半径为3,圆心角为$120^{\circ}$,则扇形的面积是(
A.$6\pi$
B.$3\pi$
C.$2\pi$
D.$\pi$
B
)A.$6\pi$
B.$3\pi$
C.$2\pi$
D.$\pi$
答案:
B
2. 某扇形的面积为$12\pi cm^{2}$,圆心角为$120^{\circ}$,则该扇形的半径是(
A.$3 cm$
B.$4 cm$
C.$5 cm$
D.$6 cm$
D
)A.$3 cm$
B.$4 cm$
C.$5 cm$
D.$6 cm$
答案:
D
3. 若扇形的半径是$12 cm$,弧长是$20\pi cm$,则扇形的面积为(
A.$120\pi cm^{2}$
B.$9\pi cm^{2}$
C.$6\pi cm^{2}$
D.$3\pi cm^{2}$
A
)A.$120\pi cm^{2}$
B.$9\pi cm^{2}$
C.$6\pi cm^{2}$
D.$3\pi cm^{2}$
答案:
A
4. 如图,$\triangle ABC内接于\odot O$,若$\angle A= 45^{\circ}$,$\odot O的半径r= 4$,则阴影部分的面积为(
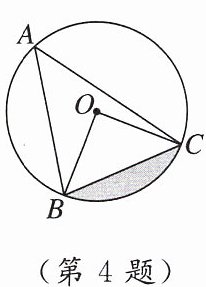
A.4
B.2
C.$4\pi - 8$
D.$4\pi - 16$
C
)
A.4
B.2
C.$4\pi - 8$
D.$4\pi - 16$
答案:
C
5. 如图,正六边形ABCDEF的边长为4,以A为圆心,AC的长为半径画弧,得$\overset{\frown}{EC}$,连结AC,AE,则图中阴影部分的面积为(
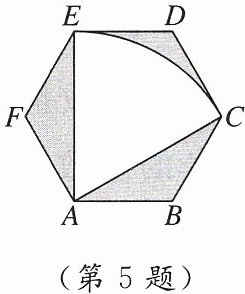
A.$24\sqrt{3} - 8\pi$
B.$8\pi$
C.$24\sqrt{3}$
D.$12\sqrt{3} - 8\pi$
A
)
A.$24\sqrt{3} - 8\pi$
B.$8\pi$
C.$24\sqrt{3}$
D.$12\sqrt{3} - 8\pi$
答案:
A
6. 情境题 地方文化 杭州西湖十景是杭州市西湖上的十处特色风景,一游客在去西湖游玩时买了一把印有西湖十景的折扇,打开后,其示意图如图,小扇形OAB的半径为$2 cm$,弧长为$\frac{5\pi}{3} cm$,大扇形OCD的半径为$26 cm$,扇面的宽度CE为$12 cm$,则扇面的面积(阴影部分)是______$cm^{2}$.(结果保留$\pi$)
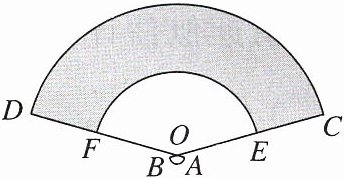

200π
答案:
200π
7. 如图所示,在$Rt\triangle ABC$中,$AB = 6 cm$,$BC = 15 cm$,分别以A,C为圆心,以AB的长为半径作圆,从$Rt\triangle ABC$中剪掉这两个半径相等的扇形,则阴影部分的面积为
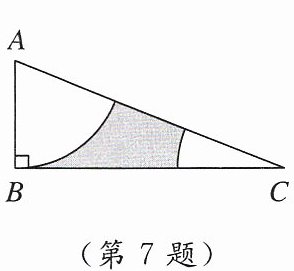
$45 - 9\pi$
$cm^{2}$.(结果保留$\pi$)
答案:
$45 - 9\pi$
8. [2025湖州月考]如图,扇形的圆心角为$120^{\circ}$,点C在圆弧上,$\angle ABC = 30^{\circ}$,$OA = 2$,则阴影部分的面积为
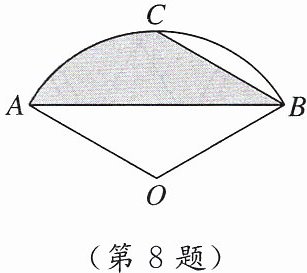
$\frac{2}{3}\pi$
.
答案:
$\frac{2}{3}\pi$
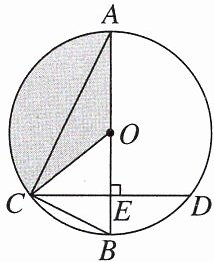
9. [2025金华月考]如图,AB是$\odot O$的直径,弦$CD\perp AB$于点E,连结AC,BC,OC.
(1)求证:$\angle ACO = \angle BCD$;
(2)若$CD = 8$,$\angle A = 30^{\circ}$,求阴影部分的面积.
(1)求证:$\angle ACO = \angle BCD$;
(2)若$CD = 8$,$\angle A = 30^{\circ}$,求阴影部分的面积.

答案:
(1)【证明】
∵AB是$\odot O$的直径,弦$CD\perp AB$,$\therefore \overset{\frown }{CB}=\overset{\frown }{DB}$,$\therefore \angle BAC=\angle BCD$.
∵OA = OC,$\therefore \angle BAC = \angle ACO$,$\therefore \angle ACO = \angle BCD$.(2)【解】
∵AB是$\odot O$的直径,弦$CD\perp AB$,CD = 8,$\therefore CE = ED = 4$.
∵$\angle A = 30^{\circ }$,$\therefore \angle COE = 60^{\circ }$,$\therefore \angle COA = 120^{\circ }$.在$\triangle OCE$中,易得$OC = \frac{8\sqrt{3}}{3}$,$\therefore$阴影部分的面积$=\frac{120\pi \left(\frac{8\sqrt{3}}{3}\right)^{2}}{360}=\frac{64\pi }{9}$.
∵AB是$\odot O$的直径,弦$CD\perp AB$,$\therefore \overset{\frown }{CB}=\overset{\frown }{DB}$,$\therefore \angle BAC=\angle BCD$.
∵OA = OC,$\therefore \angle BAC = \angle ACO$,$\therefore \angle ACO = \angle BCD$.(2)【解】
∵AB是$\odot O$的直径,弦$CD\perp AB$,CD = 8,$\therefore CE = ED = 4$.
∵$\angle A = 30^{\circ }$,$\therefore \angle COE = 60^{\circ }$,$\therefore \angle COA = 120^{\circ }$.在$\triangle OCE$中,易得$OC = \frac{8\sqrt{3}}{3}$,$\therefore$阴影部分的面积$=\frac{120\pi \left(\frac{8\sqrt{3}}{3}\right)^{2}}{360}=\frac{64\pi }{9}$.
查看更多完整答案,请扫码查看


