第49页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1 相似三角形的周长之比等于
相似比
;
答案:
相似比
2 相似三角形的面积之比等于
相似比的平方
.
答案:
相似比的平方
1. [2025 宁波鄞州区月考] 如果△ABC 与△DEF 相似且相似比是 1:2,那么△ABC 与△DEF 的周长比是(
A.2:1
B.1:√{2}
C.1:4
D.1:2
D
)A.2:1
B.1:√{2}
C.1:4
D.1:2
答案:
D
2. 已知△FHB∽△EAD,它们的周长分别为 30 和 15,且 FH= 6,则 EA 的长为(
A.3
B.2
C.4
D.5
A
)A.3
B.2
C.4
D.5
答案:
A
3. [2025 温州第二中学月考] 两个相似三角形的相似比为 2:3,它们的周长之差为 15,则周长之和是
75
.
答案:
75
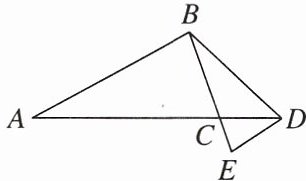
4. 如图,在△ABC 中,D 为 AC 延长线上一点,AC= 3CD,∠CBD= ∠A,过点 D 作 DE//AB 交 BC 的延长线于点 E.
(1)求证:△ECD∽△EDB;
(2)求△DCE 与△ACB 的周长比.
(1)求证:△ECD∽△EDB;
(2)求△DCE 与△ACB 的周长比.

答案:
(1)[证明]
∵DE//AB,
∴∠A=∠EDC;
∵∠CBD=∠A,
∴∠EDC=∠CBD.又
∵∠DEC=∠BED,
∴△ECD∽△EDB.
(2)[解]
∵∠A=∠EDC,∠ACB=∠DCE,
∴△DCE∽△ACB.
∴$\frac{C_{\triangle DCE}}{C_{\triangle ACB}}=\frac{CD}{AC}$.
∵AC=3CD,
∴$\frac{C_{\triangle DCE}}{C_{\triangle ACB}}=\frac{CD}{3CD}=\frac{1}{3}$,即△DCE与△ACB的周长比为1:3.
(1)[证明]
∵DE//AB,
∴∠A=∠EDC;
∵∠CBD=∠A,
∴∠EDC=∠CBD.又
∵∠DEC=∠BED,
∴△ECD∽△EDB.
(2)[解]
∵∠A=∠EDC,∠ACB=∠DCE,
∴△DCE∽△ACB.
∴$\frac{C_{\triangle DCE}}{C_{\triangle ACB}}=\frac{CD}{AC}$.
∵AC=3CD,
∴$\frac{C_{\triangle DCE}}{C_{\triangle ACB}}=\frac{CD}{3CD}=\frac{1}{3}$,即△DCE与△ACB的周长比为1:3.
5. 若两个相似三角形的相似比是 1:3,则这两个相似三角形的面积比是(
A.1:3
B.1:4
C.1:6
D.1:9
D
)A.1:3
B.1:4
C.1:6
D.1:9
答案:
D
6. 如图,在▱ABCD 中,E 为 AD 上一点,连结 AC,BE 交于点 F,S_{△AEF}:S_{△CBF}= 9:25,则 AE:ED 为(
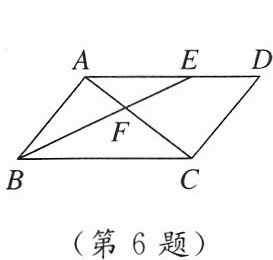
A.3:5
B.3:2
C.9:5
D.25:9
B
)
A.3:5
B.3:2
C.9:5
D.25:9
答案:
B
7. 如图,在△ABC 中,DE//BC,DB= 2AD,△ADE 的面积为 1,则△ABC 的面积为(
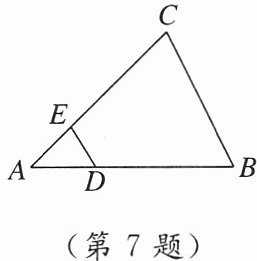
A.4
B.6
C.8
D.9
D
)
A.4
B.6
C.8
D.9
答案:
D
8. 母题 教材 P144 例 3 在比例尺为 1:10 000 的地图上有一块面积为$ 2 cm^2$的三角形空地,则它的实际面积为
20000
$m^2$.
答案:
20000
9. 如图,▱ABCD 的对角线 AC,BD 相交于点 O,E 是 CD 的中点,则$\frac{S_{△DEO}}{S_{△BCD}}= $
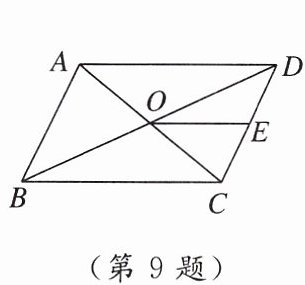
$\frac{1}{4}$
.
答案:
$\frac{1}{4}$
10. 如图,在△ABC 中,D 是边 AB 上一点,按以下步骤作图:①以点 A 为圆心,以适当长为半径作弧,分别交 AB,AC 于点 M,N;②以点 D 为圆心,以 AM 长为半径作弧,交 DB 于点 M';③以点 M'为圆心,以 MN 长为半径作弧,在∠BAC 内部交前面的弧于点 N';④过点 N'作射线 DN'交 BC 于点 E.若△BDE 与四边形 ACED 的面积比为 4:21,则$\frac{BE}{CE}$的值为

$\frac{2}{3}$
.
答案:
$\frac{2}{3}$
查看更多完整答案,请扫码查看


