《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

1. 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF有两边的长为5 cm,4 cm,若这两个三角形相似,△DEF的另一边长可以为(C)
A.3 cm
B.5 cm
C.6 cm
D.7.5 cm

答案： C

2. 若△ABC的每条边长增加各自的10%得到△A′B′C′,则∠B′的度数与其对应角∠B的度数相比(D)
A.增加了10%
B.减少了10%
C.增加了(1+10%)
D.没有改变

答案： D

3. 若△ABC的三边长分别为a,b,c,△A_1B_1C_1的三边长分别为$\sqrt{a}$,$\sqrt{b}$,$\sqrt{c}$,则△ABC与△A_1B_1C_1______不一定(填“一定”“不一定”或“一定不”)相似。

答案： 不一定

4. 如图,在△ABC与△DEF中,∠B= ∠E= 90°,则△ABC与△DEF相似吗？请说明理由。

答案： [解]△ABC与△DEF相似.理由如下:　在△ABC中,∠B=90°,AC=5,AB=4,
∴BC=3.　在△DEF中,∠E=90°,DF=10,EF=6,
∴DE=8.
∴$\frac{DF}{AC}=\frac{DE}{AB}=\frac{EF}{BC}=2$.
∴△ABC∽△DEF.

5. 如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE//AB,EF//BC,DF//AC。

求证：△DEF∽△ABC。

答案： [证明]
∵DE//AB,
∴$\frac{DE}{AB}=\frac{OE}{OB}$.
∵EF//BC,
∴$\frac{EF}{BC}=\frac{OE}{OB}$=$\frac{OF}{OC}$.
∵DF//AC,
∴$\frac{DF}{AC}=\frac{OF}{OC}$.
∴$\frac{DE}{AB}=\frac{OE}{OB}=\frac{OF}{OC}=\frac{EF}{BC}=\frac{DF}{AC}$,即$\frac{DE}{AB}=\frac{DF}{AC}=\frac{EF}{BC}$.
∴△DEF∽△ABC.

6. [2025台州月考]下列各组条件中,不能判定△ABC与△DEF相似的是(D)
A.∠A= ∠D,∠B= ∠E
B.$\frac{AB}{DE}= \frac{BC}{EF}$,∠B= ∠E
C.$\frac{AB}{DE}= \frac{BC}{EF}= \frac{AC}{DF}$
D.$\frac{AB}{DE}= \frac{AC}{DF}$,∠B= ∠E

答案： D

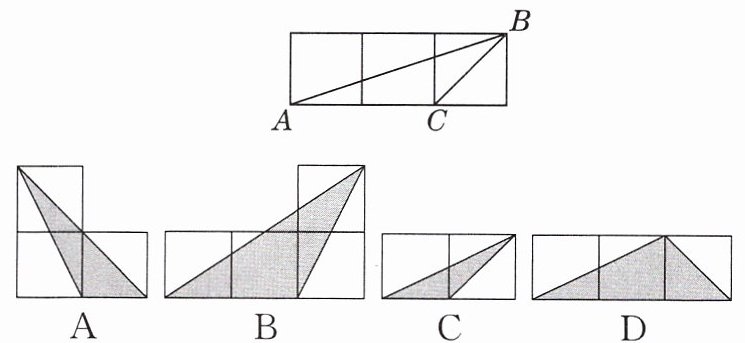
7. 如图,小正方形的边长均为1,则下列选项中的三角形(阴影部分)与△ABC相似的是(C)

答案： C

8. 如图,已知$\frac{BD}{BE}= \frac{AD}{CE}= \frac{AB}{BC}$。

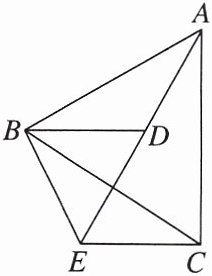
求证：△ABC∽△DBE。

答案： [证明]
∵$\frac{BD}{BE}=\frac{AD}{CE}=\frac{AB}{BC}$,
∴△ABD∽△CBE.
∴∠ABD=∠EBC.
∴∠ABC=∠EBD.
∵$\frac{BD}{BE}=\frac{AB}{BC}$,
∴$\frac{BD}{AB}=\frac{BE}{BC}$.
∴△ABC∽△DBE;