《2025年快乐暑假课程衔接组合卷七年级数学北师大版》

17. 小明站在河边的点 A 处,观察河对面(正北方向)点 B 处的一棵小树,他设计了如下方案测量自己与这棵树之间的距离,他以相同的步子先向正西方向走了 30 步到达电线杆 C 处,接着继续向正西方向走了 30 步到达 D 处,然后再向正南方向行走,当看到电线杆 C、小树 B 与自己现在所处的位置 E 在同一条直线上时停止,从 A 点出发到 E 点停止,小明共走了 100 步。
(1)根据题意,画出测量方案的示意图;
(2)如果小明一步大约 0.5 m,请计算小明在点 A 处时与这棵树之间的距离,并说明理由。

答案： 17.
(1) 图略。
(2) 小明在点 A 处时与这棵树之间的距离约为 20 m。

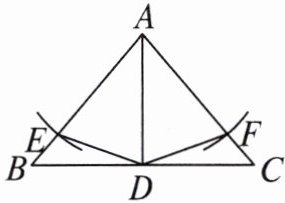
18. 如图,在$\triangle ABC$中,$AB= AC$,AD 为$\triangle ABC$的角平分线。以点 A 圆心,AD 长为半径画弧,与 AB,AC 分别交于点 E,F,连接 DE,DF。
(1)求证:$\triangle ADE\cong \triangle ADF$;
(2)若$∠BAC= 80^{\circ }$,求$∠BDE$的度数。

答案： 18.
(1) 证明: 因为 AD 是 $ \triangle ABC $ 的角平分线，所以 $ \angle BAD = \angle CAD $。
由作图知，$ AE = AF $。在 $ \triangle ADE $ 和 $ \triangle ADF $ 中，$ \begin{cases} AE = AF, \\ \angle BAD = \angle CAD, \\ AD = AD, \end{cases} $ 所以 $ \triangle ADE \cong \triangle ADF (SAS) $。
(2) $ \angle BDE = 20^{\circ} $。