2025年快乐暑假课程衔接组合卷七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假课程衔接组合卷七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
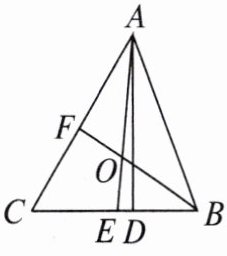
20. 如图,在$△ABC$中,AD 是高,AE,BF 是角平分线,它们相交于点 O,$∠CAB= 50^{\circ },∠C= 60^{\circ }$,求$∠DAE和∠BOA$的度数。

答案:
$ \angle DAE = 5^{\circ} $,$ \angle BOA = 120^{\circ} $。
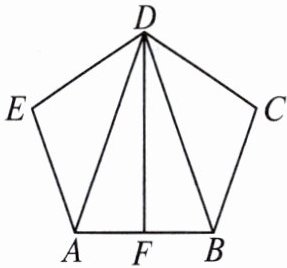
21. 如图,在五边形 ABCDE 中,$AE= BC,DE= DC,∠E= ∠C$,F 为 AB 的中点,连接 DA,DF,DB。求证:$DF⊥AB$。

答案:
证明:在 $ \triangle AED $ 和 $ \triangle BCD $ 中,$ \begin{cases} DE = DC. \\ \angle E = \angle C, \\ AE = BC, \end{cases} $ 所以 $ \triangle AED \cong \triangle BCD(SAS) $,所以 $ AD = DB $。因为 $ F $ 是 $ AB $ 的中点,所以 $ AF = BF $。在 $ \triangle AFD $ 和 $ \triangle BFD $ 中,$ \begin{cases} AD = BD, \\ AF = BF, \\ DF = DF, \end{cases} $ 所以 $ \triangle AFD \cong \triangle BFD(SSS) $,所以 $ \angle AFD = \angle DFB $。因为 $ \angle AFD + \angle DFB = 180^{\circ} $,所以 $ \angle AFD = \angle BFD = 90^{\circ} $,所以 $ DF \perp AB $。
22. 在$△ABC$中,$∠A= 60^{\circ }$,BE,CF 分别是$∠ABC和∠ACB$的平分线,CF 与 BE 相交于点 O。
(1)如图 1,若$∠ACB= 90^{\circ }$,求证:$BF+CE= BC;$
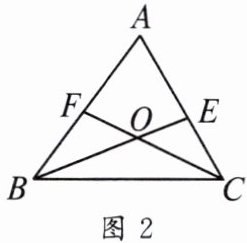
(2)如图 2,若$∠ABC与∠ACB$是任意角度,(1)中的结论是否仍成立? 请说明你的理由。
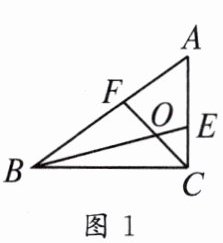
(1)如图 1,若$∠ACB= 90^{\circ }$,求证:$BF+CE= BC;$
(2)如图 2,若$∠ABC与∠ACB$是任意角度,(1)中的结论是否仍成立? 请说明你的理由。


答案:
(1) 证明:在 $ BC $ 上找到点 $ D $,使得 $ BF = BD $。因为 $ \angle A = 60^{\circ} $,$ \angle ACB = 90^{\circ} $,所以 $ \angle ABC = 30^{\circ} $。 因为 $ BE $,$ CF $ 分别是 $ \angle ABC $ 和 $ \angle ACB $ 的平分线,所以 $ \angle FBO = \angle CBO = 15^{\circ} $,$ \angle ECO = \angle BCO = 45^{\circ} $。所以 $ \triangle BOC $ 中,$ \angle BOC = 120^{\circ} $,所以 $ \angle BOF = \angle COE = 60^{\circ} $。由 $ BF = BD $,$ \angle FBO = \angle DBO $,$ BO = BO $ 可得 $ \triangle BOD \cong \triangle BOF(SAS) $,所以 $ \angle BOD = \angle BOF = 60^{\circ} $,所以 $ \angle COD = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ} $,所以 $ \angle COD = \angle COE $。由 $ \angle COD = \angle COE $,$ CO = CO $,$ \angle ECO = \angle DCO $ 可得 $ \triangle OCE \cong \triangle OCD(ASA) $,所以 $ CE = CD $。因为 $ BC = BD + CD $,所以 $ BC = BF + CE $。
因为 $ BE $,$ CF $ 分别是 $ \angle ABC $ 和 $ \angle ACB $ 的平分线,所以 $ \angle FBO = \angle CBO = 15^{\circ} $,$ \angle ECO = \angle BCO = 45^{\circ} $。所以 $ \triangle BOC $ 中,$ \angle BOC = 120^{\circ} $,所以 $ \angle BOF = \angle COE = 60^{\circ} $。由 $ BF = BD $,$ \angle FBO = \angle DBO $,$ BO = BO $ 可得 $ \triangle BOD \cong \triangle BOF(SAS) $,所以 $ \angle BOD = \angle BOF = 60^{\circ} $,所以 $ \angle COD = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ} $,所以 $ \angle COD = \angle COE $。由 $ \angle COD = \angle COE $,$ CO = CO $,$ \angle ECO = \angle DCO $ 可得 $ \triangle OCE \cong \triangle OCD(ASA) $,所以 $ CE = CD $。因为 $ BC = BD + CD $,所以 $ BC = BF + CE $。
(2) 结论 $ BC = BF + CE $ 仍成立。理由略。
(1) 证明:在 $ BC $ 上找到点 $ D $,使得 $ BF = BD $。因为 $ \angle A = 60^{\circ} $,$ \angle ACB = 90^{\circ} $,所以 $ \angle ABC = 30^{\circ} $。
 因为 $ BE $,$ CF $ 分别是 $ \angle ABC $ 和 $ \angle ACB $ 的平分线,所以 $ \angle FBO = \angle CBO = 15^{\circ} $,$ \angle ECO = \angle BCO = 45^{\circ} $。所以 $ \triangle BOC $ 中,$ \angle BOC = 120^{\circ} $,所以 $ \angle BOF = \angle COE = 60^{\circ} $。由 $ BF = BD $,$ \angle FBO = \angle DBO $,$ BO = BO $ 可得 $ \triangle BOD \cong \triangle BOF(SAS) $,所以 $ \angle BOD = \angle BOF = 60^{\circ} $,所以 $ \angle COD = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ} $,所以 $ \angle COD = \angle COE $。由 $ \angle COD = \angle COE $,$ CO = CO $,$ \angle ECO = \angle DCO $ 可得 $ \triangle OCE \cong \triangle OCD(ASA) $,所以 $ CE = CD $。因为 $ BC = BD + CD $,所以 $ BC = BF + CE $。
因为 $ BE $,$ CF $ 分别是 $ \angle ABC $ 和 $ \angle ACB $ 的平分线,所以 $ \angle FBO = \angle CBO = 15^{\circ} $,$ \angle ECO = \angle BCO = 45^{\circ} $。所以 $ \triangle BOC $ 中,$ \angle BOC = 120^{\circ} $,所以 $ \angle BOF = \angle COE = 60^{\circ} $。由 $ BF = BD $,$ \angle FBO = \angle DBO $,$ BO = BO $ 可得 $ \triangle BOD \cong \triangle BOF(SAS) $,所以 $ \angle BOD = \angle BOF = 60^{\circ} $,所以 $ \angle COD = 180^{\circ} - 60^{\circ} - 60^{\circ} = 60^{\circ} $,所以 $ \angle COD = \angle COE $。由 $ \angle COD = \angle COE $,$ CO = CO $,$ \angle ECO = \angle DCO $ 可得 $ \triangle OCE \cong \triangle OCD(ASA) $,所以 $ CE = CD $。因为 $ BC = BD + CD $,所以 $ BC = BF + CE $。(2) 结论 $ BC = BF + CE $ 仍成立。理由略。
查看更多完整答案,请扫码查看


