2025年快乐暑假课程衔接组合卷七年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假课程衔接组合卷七年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
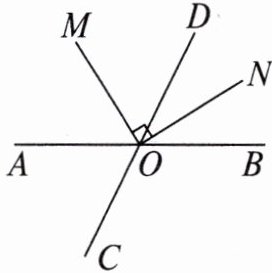
17. 如图,直线 AB,CD 相交于点 O,ON 平分$∠BOD,OM⊥ON$。
(1)若$∠AOC= 64^{\circ }$,求$∠MOB$的度数;
(2)试说明 OM 平分$∠AOD$。
(1)若$∠AOC= 64^{\circ }$,求$∠MOB$的度数;
(2)试说明 OM 平分$∠AOD$。

答案:
(1)$ \angle M O B = 122 ^ { \circ } $。
(2)
(1)$ \angle M O B = 122 ^ { \circ } $。
(2)

18. 如图,直线$AB// CD$,点 E 在直线 AB 上,点 F 在直线 CD 上,点 P 在直线 AB,CD 之间,连接 PE,PF,EF,$∠PFE= 50^{\circ }$,直线 l 与直线 AB,CD 分别交于点 M,N,$∠MNC= α(0^{\circ }<α<90^{\circ })$,EO 是$∠MEF$的平分线,交直线 CD 于点 O。
(1)求证:$∠AEP+∠PFC= ∠EPF$;
(2)若$PF// MN,OE// MN$,求α;
(3)将直线 l 向左平移,并保持$PF// MN$,在平移的过程中(点 M 与点 E 不重合时),求$∠EOF$的度数(用含α的式子表示)。
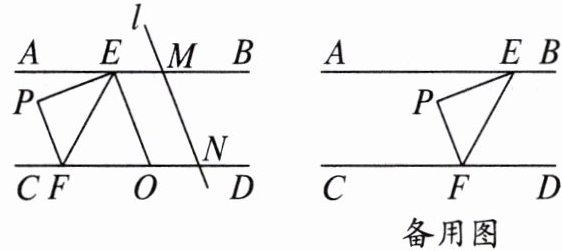
(1)求证:$∠AEP+∠PFC= ∠EPF$;
(2)若$PF// MN,OE// MN$,求α;
(3)将直线 l 向左平移,并保持$PF// MN$,在平移的过程中(点 M 与点 E 不重合时),求$∠EOF$的度数(用含α的式子表示)。
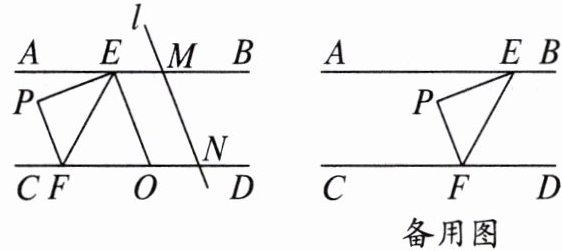
答案:
(1)证明:因为 $ A B // C D $,所以 $ \angle A E F + \angle C F E = 180 ^ { \circ } $,
所以 $ \angle A E P + \angle P E F + \angle P F E + \angle P F C = 180 ^ { \circ } $。
因为 $ \angle P E F + \angle P F E + \angle E P F = 180 ^ { \circ } $,
所以 $ \angle A E P + \angle P F C = \angle E P F $。
(2)$ \alpha = 50 ^ { \circ } $。
(3)$ \angle E O F $ 的度数为 $ \frac { 1 } { 2 } \alpha + 25 ^ { \circ } $ 或 $ 65 ^ { \circ } - \frac { 1 } { 2 } \alpha $。
(1)证明:因为 $ A B // C D $,所以 $ \angle A E F + \angle C F E = 180 ^ { \circ } $,
所以 $ \angle A E P + \angle P E F + \angle P F E + \angle P F C = 180 ^ { \circ } $。
因为 $ \angle P E F + \angle P F E + \angle E P F = 180 ^ { \circ } $,
所以 $ \angle A E P + \angle P F C = \angle E P F $。
(2)$ \alpha = 50 ^ { \circ } $。
(3)$ \angle E O F $ 的度数为 $ \frac { 1 } { 2 } \alpha + 25 ^ { \circ } $ 或 $ 65 ^ { \circ } - \frac { 1 } { 2 } \alpha $。
查看更多完整答案,请扫码查看


