《2025年快乐暑假课程衔接组合卷七年级数学北师大版》

14. 如图,在$△ABC$中,$AB= AC,∠BAC= 120^{\circ }$,D,E是BC边上的点,连接AD,AE,作$△AD'E$,使$△AD'E与△ADE$关于边AE所在直线对称,连接$D'C$。若$BD= $$CD'$,则$∠DAE= $60^{\circ}。

答案： $60^{\circ}$

15. 如图,现准备在一条公路旁修建一个仓储基地,分别给A,B两个超市配货,那么这个基地建在什么位置,才能使它到两个超市的距离之和最小？(保留作图痕迹及简要说明)

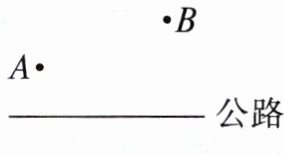
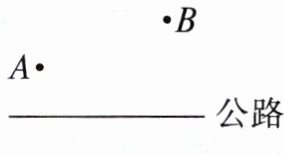
答案：
如图，作点 $B$ 关于公路的对称点 $B'$，连接 $AB'$，交公路于点 $C$，则这个基地建在 $C$ 处，才能使它到这两个超市的距离之和最小。

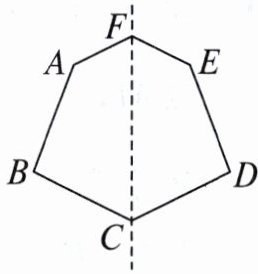
16. 如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴。若$∠AFC+∠BCF= 150^{\circ }$,求$∠AFE+∠BCD$的大小。

答案： $ \angle AFE + \angle BCD = 300^{\circ}$。

17. 一犯罪嫌疑人正在两交叉公路(OM和ON)间沿到两公路距离相等的一条小路上逃跑,埋伏在A,B两处的两名公安人员想在距A,B相等的距离处同时抓住这一犯罪嫌疑人(如图)。请你帮助公安人员在图中设计出抓捕点,并说明理由。(保留作图痕迹)

答案：
如图，作 $ \angle MON$ 的平分线 $OC$，连接 $AB$，作线段 $AB$ 的垂直平分线，与 $OC$ 交于点 $P$，则点 $P$ 为抓捕点。理由略。