《2025年快乐暑假课程衔接组合卷七年级数学北师大版》

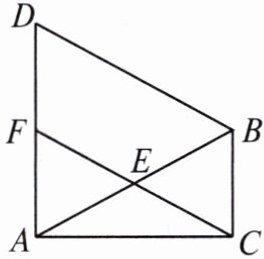
19. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle CAB = 30^{\circ}$,以$AB为边在\triangle ABC外作等边三角形ABD$,$E是AB$的中点,连接$CE并延长交AD于点F$。
求证：$\triangle AEF\cong\triangle BEC$。

答案： 证明:因为 $ \triangle ABD $ 是等边三角形，所以 $ \angle FAE = 60 ^ { \circ } $。
因为 $ \angle CAB = 30 ^ { \circ } $，$ \angle ACB = 90 ^ { \circ } $，
所以 $ \angle EBC = 180 ^ { \circ } - 90 ^ { \circ } - 30 ^ { \circ } = 60 ^ { \circ } $，所以 $ \angle FAE = \angle EBC $。
因为 $ E $ 为 $ AB $ 的中点，所以 $ AE = BE $。
在 $ \triangle AEF $ 和 $ \triangle BEC $ 中，$ \left\{ \begin{array} { l } { \angle FAE = \angle EBC , } \\ { AE = BE , } \\ { \angle FEA = \angle BEC , } \end{array} \right. $ 所以 $ \triangle AEF \cong \triangle BEC ( \mathrm { ASA } ) $。

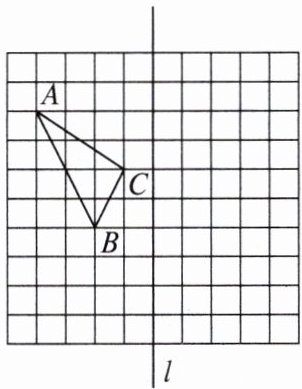
20. 在如图所示的正方形网格中,每个小正方形的边长为$1$,$\triangle ABC$的顶点都在正方形网格的格点(网格线的交点)上。
(1)请作出$\triangle ABC关于直线l对称的\triangle A_1B_1C_1$；(点$A_1$,$B_1$,$C_1分别为点A$,$B$,$C$的对应点)；
(2)在直线$l上找一点P$,使$PA + PC$最小。(保留作图痕迹,在图中标出点$P$)

答案：

(1)如图，$ \triangle A _ { 1 } B _ { 1 } C _ { 1 } $ 即为所求。
(2)如图，点 $ P $ 即为所求。

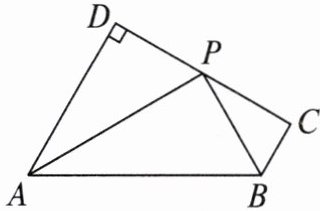
21. 如图,在四边形$ABCD$中,$AD// BC$,$\angle D = 90^{\circ}$,$\angle DAB的平分线与\angle CBA的平分线相交于点P$,且点$P在线段CD$上,$\angle CPB = 30^{\circ}$。
(1)求$\angle PAD$的度数；
(2)试说明：$PD = PC$。

答案：

1.