《2025年快乐暑假课程衔接组合卷七年级数学北师大版》

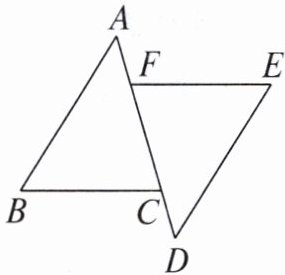
16. 如图,$FE// BC$,点 C,F 在 AD 上,$∠B= ∠E,DC= AF$,求证:$AB// DE$。

答案： 证明:因为$FE// BC$,所以$\angle DFE=\angle ACB$。
因为$\angle B=\angle E,\angle D=180^{\circ}-\angle DFE-\angle E$,
$\angle A=180^{\circ}-\angle ACB-\angle B$,
所以$\angle D=\angle A$,所以$AB// DE$。

17. 如图,两个边长相等的正方形,把正方形 EFGH 的顶点 E 放在正方形 ABCD 的中心,正方形 ABCD 固定不动,另一个正方形 EFGH 绕中心 E 旋转。
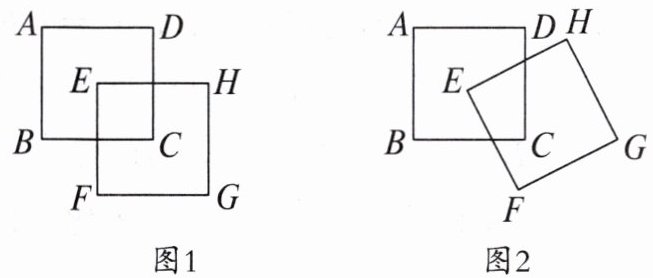
(1)如图 1,当正方形 ABCD 的边长为 6 时,两个正方形重叠部分的面积是9;
(2)在(1)的条件下,当正方形 EFGH 绕中心 E 旋转成图 2 的位置,两个正方形重叠部分的面积是否发生变化? 请说明理由;
(3)当正方形 ABCD 的边长为 a 时,在正方形 EFGH 绕中心 E 旋转的过程中,请直接写出两个正方形重叠部分的面积。

答案：
(1)9
(2)两个正方形重叠部分的面积没有发生变化,还是 9。理由略。
(3)$\frac{1}{4}a^{2}$。