《2025年复习计划风向标暑八年级数学北师大版》

12. 按一定规律排列的单项式$a,-2\sqrt{2}a^2,3\sqrt{3}a^3,-8a^4,…$,第$n$($n$为正整数)个单项式是______.

答案： $(-1)^{n+1}\sqrt[n]{n}a^{n}$

13. 若$a= \frac{2}{\sqrt{3}-1}$,则$\frac{1}{2}a^3-a^2-a+2= $______.

答案： 2

14. 如图,大、小两个正方形并排放在一起,大正方形的边长为10,小正方形的边长为6,则阴影部分的面积为______.

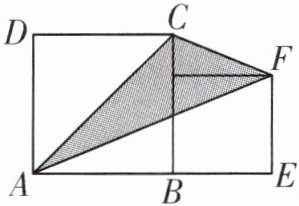
答案： 50

15. (8分)计算:
(1)$(\sqrt{3}-2)^2+\sqrt{12}+6\sqrt{\frac{1}{3}}$;
(2)$(-2)^2-|-3|+\sqrt{2}×\sqrt{8}+(-6)^0$;
(3)$(1-\pi)^0+|\sqrt{2}-\sqrt{3}|-\sqrt{12}+(\frac{1}{\sqrt{2}})^{-1}$;
(4)$(2\sqrt{3}-1)(\sqrt{3}+1)-(1-2\sqrt{3})^2$.

答案： 解:
(1)原式$=3+4-4\sqrt{3}+2\sqrt{3}+6×\frac{\sqrt{3}}{3}=3+4-4\sqrt{3}+2\sqrt{3}+2\sqrt{3}=7$.
(2)原式$=4-3+4+1=6$.
(3)原式$=1+\sqrt{3}-\sqrt{2}-2\sqrt{3}+\sqrt{2}=1-\sqrt{3}$.
(4)原式$=6+2\sqrt{3}-\sqrt{3}-1-(1-4\sqrt{3}+12)=6+2\sqrt{3}-\sqrt{3}-1-13+4\sqrt{3}=-8+5\sqrt{3}$.

16. (8分)在解决问题“已知$a= \frac{1}{\sqrt{2}-1}$,求$2a^2-4a+1$的值”时,小明是这样分析与解答的:
$\because a= \frac{1}{\sqrt{2}-1}= \frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}= \sqrt{2}+1,\therefore a-1= \sqrt{2}$.
$\therefore (a-1)^2= 2.\therefore a^2-2a+1= 2.\therefore a^2-2a= 1$.
$\therefore 2a^2-4a= 2.\therefore 2a^2-4a+1= 3$.
请你根据小明的分析过程,解决如下问题:
(1)化简:$\frac{2}{3-\sqrt{7}}$;
(2)若$a= \frac{1}{3+2\sqrt{2}}$,求$3a^2-18a-1$的值.

答案： 解:
(1)原式$=\frac{2(3+\sqrt{7})}{(3-\sqrt{7})(3+\sqrt{7})}=\frac{2(3+\sqrt{7})}{9-7}=3+\sqrt{7}$.
(2)$\because a=\frac{3-2\sqrt{2}}{(3+2\sqrt{2})(3-2\sqrt{2})}=\frac{3-2\sqrt{2}}{9-8}=3-2\sqrt{2}$,$\therefore a-3=-2\sqrt{2}$.$\therefore (a-3)^{2}=8$.$\therefore a^{2}-6a+9=8$.$\therefore a^{2}-6a=-1$.$\therefore 3a^{2}-18a-1=3(a^{2}-6a)-1=3×(-1)-1=-4$.