《2025年复习计划风向标暑八年级数学北师大版》

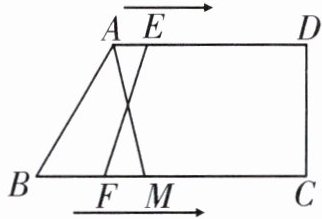
5. 在四边形 $ABCD$ 中,$AD // BC$,$BC \perp CD$,$BC = 10\ \text{cm}$,$M$ 是 $BC$ 上一点,且 $BM = 4\ \text{cm}$,点 $E$ 从 $A$ 出发以 $1\ \text{cm/s}$ 的速度向 $D$ 运动,点 $F$ 从点 $B$ 出发以 $2\ \text{cm/s}$ 的速度向点 $C$ 运动,当其中一点到达终点,则另一点也随之停止运动,设运动时间为 $t\ \text{s}$,当 $t$ 的值为______时,以 $A$,$M$,$E$,$F$ 为顶点的四边形是平行四边形。

答案： 4 或 $\frac{4}{3}$

6. 如图,$□ ABCD$ 的对角线 $AC$ 与 $BD$ 相交于点 $O$,$E$,$F$ 是 $BD$ 上的两点。
(1) 当 $BE$,$DF$ 满足什么条件时,四边形 $AECF$ 是平行四边形？请说明理由；
(2) 当 $\angle AEB$ 与 $\angle CFD$ 满足什么条件时,四边形 $AECF$ 是平行四边形？请说明理由。

答案： 解:
(1)BE=DF,理由:
∵ 四边形 ABCD 是平行四边形,
∴ BO =DO,AO =CO.
∵ BE=DF,
∴ BO - BE =DO - DF,
∴ OE =OF,
∴ 四边形 AECF 是平行四边形.
(2)∠AEB =∠CFD,理由:
∵ 四边形 ABCD 是平行四边形,
∴ AB =CD,AB//CD,
∴ ∠ABE =∠CDF.又
∵ ∠AEB =∠CFD,
∴ △ABE≌△CDF(AAS),
∴ AE =CF.
∵ ∠AEB =∠CFD,
∴ ∠AEF =∠CFE,
∴ AE//CF,
∴ 四边形 AECF 是平行四边形.

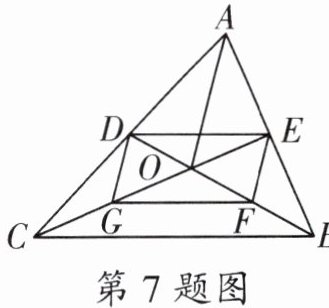
7. 如图,$\triangle ABC$ 的中线 $BD$,$CE$ 交于点 $O$,连接 $OA$,点 $G$,$F$ 分别为 $OC$,$OB$ 的中点,$BC = 8$,$AO = 6$,则四边形 $DEFG$ 的周长为______。

答案： 14

8. 如图,在 $\triangle ABC$ 中,$BF$ 平分 $\angle ABC$,$AF \perp BF$ 于点 $F$,$D$ 为 $AB$ 的中点,连接 $DF$ 并延长交 $AC$ 于点 $E$。若 $AB = 20$,$BC = 32$,则线段 $EF$ 的长为______。

答案： 6

9. 如图,四边形 $ABCD$ 中,$\angle A = 60^{\circ}$,$AD = 2$,$AB = 3$,点 $M$,$N$ 分别为线段 $BC$,$AB$ 上的动点(含端点,但点 $M$ 不与点 $B$ 重合),点 $E$,$F$ 分别为 $DM$,$MN$ 的中点,则 $EF$ 长度的最大值为______。

答案： $\frac{\sqrt{7}}{2}$