《2025年复习计划风向标暑八年级数学北师大版》

6. 如图,过正方形ABCD的顶点B作直线l,过A,C作直线l的垂线,垂足分别为E,F,若AE= 1,CF= 3,则AB的长为 ( )


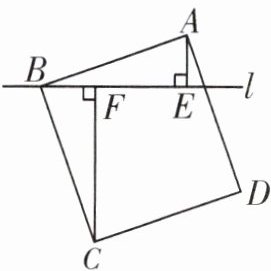
A.$ \sqrt { 10 } $
B.10
C.3
D.$ \sqrt { 5 } $

答案： A

7. 操作:将一把三角尺放在如图1的正方形ABCD中,使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.
探究:
(1)如图2,当点Q在DC上时,求证:PQ= PB;
(2)如图3,当点Q在DC延长线上时,(1)中的结论还成立吗? 简要说明理由.

答案：

(1)证明:如题图2,过点 P 作$PN⊥AB$于点 N,延长 PN 交 CD 于点 M,在正方形 ABCD 中,$AB// CD$,$∠ACD=45^{\circ }$,
∴ $∠PMQ=∠BNP=∠CBN=90^{\circ }$.
∴ 四边形 CBNM 是矩形.
∴ $CM=BN$.
∴ $\triangle CMP$是等腰直角三角形.
∴ $PM=CM=BN$.
∵ $∠NBP+∠BPN=90^{\circ }$,$∠BPN+∠MPQ=90^{\circ }$,
∴ $∠MPQ=∠NBP$.在$\triangle PMQ$和$\triangle BNP$中,$\left\{\begin{array}{l} ∠MPQ=∠NBP\\ PM=BN\\ ∠PMQ=∠BNP\end{array}\right. $,
∴ $\triangle PMQ\cong \triangle BNP$(ASA).
∴ $PQ=PB$.

(2)解:成立.理由:如题图3,过点 P 作$PN⊥AB$于点 N,延长 PN 交 CD 于点 M,在正方形 ABCD 中,$AB// CD$,$∠ACD=45^{\circ }$,
∴ $∠PMQ=∠BNP=∠CBN=90^{\circ }$.
∴ 四边形 CBNM 是矩形.
∴ $CM=BN$.
∴ $\triangle CMP$是等腰直角三角形.
∴ $PM=CM=BN$.
∵ $∠NBP+∠BPN=90^{\circ }$,$∠BPN+∠MPQ=90^{\circ }$,
∴ $∠MPQ=∠NBP$.在$\triangle PMQ$和$\triangle BNP$中,$\left\{\begin{array}{l} ∠MPQ=∠NBP\\ PM=BN\\ ∠PMQ=∠BNP\end{array}\right. $,
∴ $\triangle PMQ\cong \triangle BNP$(ASA).
∴ $PQ=PB$.