《2025年复习计划风向标暑八年级数学北师大版》

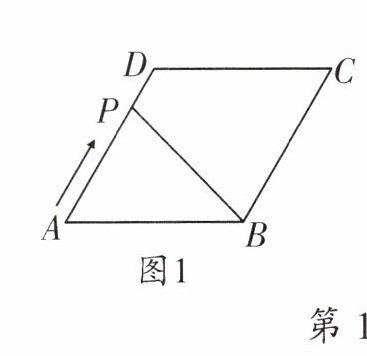
19. 如图 1,在菱形$ABCD$中,$\angle A = 60^\circ$,动点$P从点A$出发,沿折线$AD \to DC \to CB$方向匀速运动,运动到点$B$停止,设点$P的运动路程为x$,$\triangle APB的面积为y$,$y与x$的函数图象如图 2 所示,则$AB$的长为 ( )

A.$\sqrt{3}$
B.$2\sqrt{3}$
C.$3\sqrt{3}$
D.$4\sqrt{3}$

答案： B

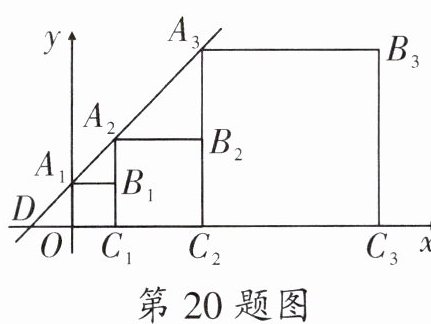
20. 如图,直线$y = x + 1与x轴交于点D$,与$y轴交于点A_1$,把正方形$A_1B_1C_1O$,$A_2B_2C_2C_1和A_3B_3C_3C_2$按如图所示方式放置,点$A_2$,$A_3在直线y = x + 1$上,点$C_1$,$C_2$,$C_3在x$轴上,按照这样的规律,则正方形$A_{2023}B_{2023}C_{2023}C_{2022}中的点B_{2023}$的坐标为______.

答案： $ (2^{2023}-1,2^{2022}) $

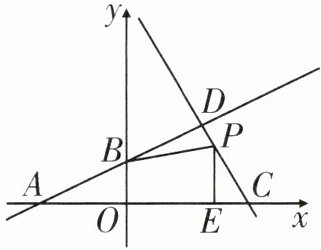
21. 如图,在平面直角坐标系中,直线$y = \frac{1}{2}x + 2与x$轴、$y轴的交点分别为A$,$B$,直线$y = - 2x + 12交x轴于点C$,两条直线的交点为$D$.点$P是线段DC$上的一个动点(不与点$C$重合),过点$P作PE \perp x$轴,交$x轴于点E$,连接$BP$.
(1)求$\triangle DAC$的面积；
(2)在线段$DC上是否存在一点P$,使四边形$BOEP$为矩形? 若存在,写出点$P$的坐标；若不存在,说明理由；
(3)若四边形$BOEP的面积为S$,设点$P的坐标为(x,y)$,求出$S关于x$的函数关系式,并写出自变量$x$的取值范围.

答案： 解:
(1)令$ y=\frac{1}{2}x+2=0 $,得x=-4.
∴点A的坐标为(-4,0).令$ y=-2x+12=0 $,得x=6.
∴点C的坐标为(6,0).联立$\left\{\begin{array}{l} y=\frac{1}{2}x+2,\\ y=-2x+12,\end{array}\right.$解得$\left\{\begin{array}{l} x=4,\\ y=4.\end{array}\right.$
∴点D的坐标为(4,4).
∴$ S_{\triangle DAC}=\frac{1}{2}×10×4=20 $.
(2)存在.
∵四边形BOEP为矩形,
∴BO=PE.在$ y=\frac{1}{2}x+2 $中,当x=0时,y=2,点B的坐标为(0,2).把y=2代入$ y=-2x+12 $得到x=5,
∴点P的坐标是(5,2).
(3)
∵$ S=\frac{1}{2}(OB+PE)\cdot OE $,
∴$ S=\frac{1}{2}(2+y)\cdot x=\frac{1}{2}(2-2x+12)\cdot x=-x^{2}+7x(4\leqslant x＜6) $.