2025年复习计划风向标暑八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习计划风向标暑八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
10. 如图,正方形ABCD与正方形BEFG有公共顶点B,连接EC,GA,交于点O,GA与BC交于点P,连接OD,OB,则下列结论一定正确的是 ( )
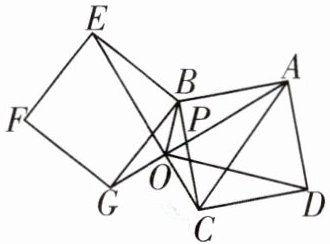
①EC⊥AG;②EC= AG;③BO平分∠CBG;④∠OBC= ∠OAC.
A.①③
B.①②③
C.②③
D.①②④

①EC⊥AG;②EC= AG;③BO平分∠CBG;④∠OBC= ∠OAC.
A.①③
B.①②③
C.②③
D.①②④
答案:
D
11. 在数学活动课中,小辉将边长为$ \sqrt { 2 } $和3的两个正方形放置在直线l上,如图1,连接AD,CF,经测量发现AD= CF.
(1)小辉将正方形ODEF绕点O逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗? 说明你的理由;
(2)小辉将正方形ODEF绕点O逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.

(1)小辉将正方形ODEF绕点O逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗? 说明你的理由;
(2)小辉将正方形ODEF绕点O逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.

答案:
解:
(1)$AD=CF$.理由如下:在正方形 ABCO 和正方形 ODEF 中,$AO=CO$,$OD=OF$,$∠AOC=∠DOF=90^{\circ }$,
∴ $∠AOC+∠COD=∠DOF+∠COD$,即$∠AOD=∠COF$.
∴ $\triangle AOD\cong \triangle COF$(SAS).
∴ $AD=CF$.
(2)与
(1)同理得到$CF=AD$,如图,连接 DF 交 OE 于点 G,则$DF⊥OE$,$DG=OG=\frac{1}{2}OE$.
∵ 正方形 ODEF 的边长为$\sqrt{2}$,
∴ $OE=\sqrt{2}×\sqrt{2}=2$.
∴ $DG=1$.
∴ $AG=AO + OG=3+1=4$.在$Rt\triangle ADG$中,$AD=\sqrt{AG^{2}+DG^{2}}=\sqrt{17}$,
∴ $CF=AD=\sqrt{17}$.

解:
(1)$AD=CF$.理由如下:在正方形 ABCO 和正方形 ODEF 中,$AO=CO$,$OD=OF$,$∠AOC=∠DOF=90^{\circ }$,
∴ $∠AOC+∠COD=∠DOF+∠COD$,即$∠AOD=∠COF$.
∴ $\triangle AOD\cong \triangle COF$(SAS).
∴ $AD=CF$.
(2)与
(1)同理得到$CF=AD$,如图,连接 DF 交 OE 于点 G,则$DF⊥OE$,$DG=OG=\frac{1}{2}OE$.
∵ 正方形 ODEF 的边长为$\sqrt{2}$,
∴ $OE=\sqrt{2}×\sqrt{2}=2$.
∴ $DG=1$.
∴ $AG=AO + OG=3+1=4$.在$Rt\triangle ADG$中,$AD=\sqrt{AG^{2}+DG^{2}}=\sqrt{17}$,
∴ $CF=AD=\sqrt{17}$.

查看更多完整答案,请扫码查看


