2025年复习计划风向标暑八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习计划风向标暑八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
14. 漏刻是我国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人民对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究中发现水位$h(cm)是时间t(min)$的一次函数,且当时间$t = 0 min$时,水位$h = 2 cm$.如表是小明记录的部分数据,其中有一个$h$的值记录不符合题意,请排除后利用正确的数据确定当$h为8 cm$时,对应的时间$t$为______$min$.


答案:
15
15. (8分)如图,在平面直角坐标系中,点$A$,$B的坐标分别为(-\frac{\sqrt{3}}{2},0)$,$(\frac{\sqrt{3}}{2},1)$,连接$AB$,以$AB为边向上作等边三角形ABC$,且$CA \perp x$轴.
(1)求点$C$的坐标;
(2)求线段$BC$所在直线的解析式.

(1)求点$C$的坐标;
(2)求线段$BC$所在直线的解析式.

答案:
解:
(1)如图,过点B作BH⊥x轴于点H,
∵点A的坐标为(−$\frac{\sqrt{3}}{2}$,0),点B的坐标为($\frac{\sqrt{3}}{2}$,1),
∴AH=$\sqrt{3}$,BH=1,
∴AB=$\sqrt{AH^{2}+BH^{2}}$=2.
∵BH=1,
∴∠BAH=30°.
∵△ABC为等边三角形,且CA⊥x轴,
∴AB=AC=2,∠CAH=90°,
∴点C的坐标为(−$\frac{\sqrt{3}}{2}$,2).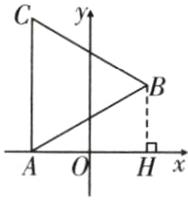
(2)由
(1)知点C的坐标为(−$\frac{\sqrt{3}}{2}$,2),又
∵点B的坐标为($\frac{\sqrt{3}}{2}$,1),设线段BC所在直线的解析式为y=kx+b(k≠0),则$\begin{cases} 1=\frac{\sqrt{3}}{2}k+b, \\ 2=-\frac{\sqrt{3}}{2}k+b, \end{cases}$解得$\begin{cases} k=-\frac{\sqrt{3}}{3}, \\ b=\frac{3}{2}. \end{cases}$
∴线段BC所在直线的解析式为$y=-\frac{\sqrt{3}}{3}x+\frac{3}{2}$.
解:
(1)如图,过点B作BH⊥x轴于点H,
∵点A的坐标为(−$\frac{\sqrt{3}}{2}$,0),点B的坐标为($\frac{\sqrt{3}}{2}$,1),
∴AH=$\sqrt{3}$,BH=1,
∴AB=$\sqrt{AH^{2}+BH^{2}}$=2.
∵BH=1,
∴∠BAH=30°.
∵△ABC为等边三角形,且CA⊥x轴,
∴AB=AC=2,∠CAH=90°,
∴点C的坐标为(−$\frac{\sqrt{3}}{2}$,2).

(2)由
(1)知点C的坐标为(−$\frac{\sqrt{3}}{2}$,2),又
∵点B的坐标为($\frac{\sqrt{3}}{2}$,1),设线段BC所在直线的解析式为y=kx+b(k≠0),则$\begin{cases} 1=\frac{\sqrt{3}}{2}k+b, \\ 2=-\frac{\sqrt{3}}{2}k+b, \end{cases}$解得$\begin{cases} k=-\frac{\sqrt{3}}{3}, \\ b=\frac{3}{2}. \end{cases}$
∴线段BC所在直线的解析式为$y=-\frac{\sqrt{3}}{3}x+\frac{3}{2}$.
16. (12分)某商店准备购进$A$,$B$两种商品,$A种商品每件的进价比B种商品每件的进价多20$元,用$3000元购进A种商品和用1800元购进B$种商品的数量相同.商店将$A种商品每件的售价定为80$元,$B种商品每件的售价定为45$元.
(1)$A$种商品每件的进价为______元,$B$种商品每件的进价为______元;
(2)商店计划用不超过$1560元的资金购进A$,$B两种商品共40$件,其中$A种商品的数量不低于B$种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件$A种商品售价优惠m(10 < m < 20)$元,$B$种商品售价不变,在(2)条件下,请设计出销售这$40$件商品获得总利润最大的进货方案.
(1)$A$种商品每件的进价为______元,$B$种商品每件的进价为______元;
(2)商店计划用不超过$1560元的资金购进A$,$B两种商品共40$件,其中$A种商品的数量不低于B$种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件$A种商品售价优惠m(10 < m < 20)$元,$B$种商品售价不变,在(2)条件下,请设计出销售这$40$件商品获得总利润最大的进货方案.
答案:
解:
(1)50 30
(2)设购买A种商品a件,则购买B种商品(40 - a)件,由题意,得$\begin{cases} 50a+30(40 - a)\leq1560, \\ a\geq\frac{40 - a}{2}, \end{cases}$解得$\frac{40}{3}\leq a\leq18$.
∵a为正整数,
∴a = 14,15,16,17,18,
∴该商店共有5种进货方案.
(3)设销售A,B两种商品共获利y元,由题意得y=(80 - 50 - m)a+(45 - 30)(40 - a)=(15 - m)a+600.①当10 < m < 15时,15 - m > 0,y随a的增大而增大,
∴当a = 18时,获利最大,即购进18件A种商品,22件B种商品;②当m = 15时,15 - m = 0,y与a的值无关,即
(2)问中所有进货方案获利相同;③当15 < m < 20时,15 - m < 0,y随a的增大而减小,
∴当a = 14时,获利最大,即购进14件A种商品,26件B种商品.
(1)50 30
(2)设购买A种商品a件,则购买B种商品(40 - a)件,由题意,得$\begin{cases} 50a+30(40 - a)\leq1560, \\ a\geq\frac{40 - a}{2}, \end{cases}$解得$\frac{40}{3}\leq a\leq18$.
∵a为正整数,
∴a = 14,15,16,17,18,
∴该商店共有5种进货方案.
(3)设销售A,B两种商品共获利y元,由题意得y=(80 - 50 - m)a+(45 - 30)(40 - a)=(15 - m)a+600.①当10 < m < 15时,15 - m > 0,y随a的增大而增大,
∴当a = 18时,获利最大,即购进18件A种商品,22件B种商品;②当m = 15时,15 - m = 0,y与a的值无关,即
(2)问中所有进货方案获利相同;③当15 < m < 20时,15 - m < 0,y随a的增大而减小,
∴当a = 14时,获利最大,即购进14件A种商品,26件B种商品.
查看更多完整答案,请扫码查看


