《2025年复习计划风向标暑八年级数学北师大版》

1. 将一张矩形纸片 $ABCD$ 按如图所示的方式折叠,$AE$,$AF$ 为折痕,点 $B$,$D$ 折叠后的对应点分别为 $B'$,$D'$,若 $\angle B'AD' = 10^{\circ}$,则 $\angle EAF$ 的度数为______.

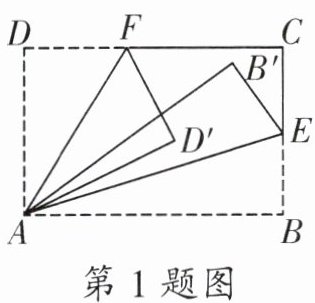
答案： 40°

2. 如图,已知点 $E$ 是矩形 $ABCD$ 中 $AD$ 边上一点,将四边形 $BCDE$ 沿直线 $BE$ 折叠,折叠后点 $C$ 的对应点为 $C'$,点 $D$ 的对应点为 $D'$,若点 $A$ 在 $C'D'$ 上,且 $AB = 10$,$BC = 8$,则 $AE= $______.

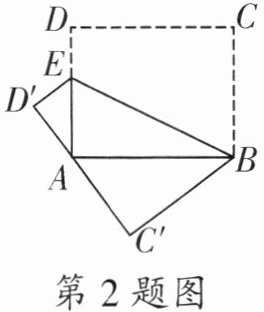
答案： 5

3. 如图,在平行四边形 $ABCD$ 中,$AB = 2$,$AD = 1$,$\angle ADC = 60^{\circ}$,将平行四边形 $ABCD$ 沿过点 $A$ 的直线 $l$ 折叠,使点 $D$ 落到 $AB$ 边上的点 $D'$ 处,折痕交 $CD$ 边于点 $E$。若点 $P$ 是直线 $l$ 上的一个动点,则 $PD' + PB$ 的最小值为______.

答案： $\sqrt{7}$

4. 综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.
(1)操作判断
操作一：对折矩形纸片 $ABCD$,使 $AD$ 与 $BC$ 重合,得到折痕 $EF$,把纸片展平；
操作二：在 $AD$ 上选一点 $P$,沿 $BP$ 折叠,使点 $A$ 落在矩形内部点 $M$ 处,把纸片展平,连接 $PM$,$BM$.
根据以上操作,当点 $M$ 在 $EF$ 上时,写出图 1 中一个 $30^{\circ}$ 的角：______.
(2)迁移探究
小华将矩形纸片换成正方形纸片,继续探究,过程如下：
将正方形纸片 $ABCD$ 按照(1)中的方式操作,并延长 $PM$ 交 $CD$ 于点 $Q$,连接 $BQ$.
①如图 2,当点 $M$ 在 $EF$ 上时,$\angle MBQ= $______$^{\circ}$,$\angle CBQ= $______$^{\circ}$.
②改变点 $P$ 在 $AD$ 上的位置(点 $P$ 不与点 $A$,$D$ 重合),如图 3,判断 $\angle MBQ$ 与 $\angle CBQ$ 的数量关系,并说明理由.
(3)拓展应用
在(2)的探究中,已知正方形纸片 $ABCD$ 的边长为 $8cm$,当 $FQ = 1cm$ 时,直接写出 $AP$ 的长.

答案： 解:
(1)∠ABP 或∠PBM 或∠MBC 或∠BME.(注:任意写出一个即可)
(2)①15 15 ②∠MBQ=∠CBQ.理由如下:
∵ 四边形ABCD是正方形,
∴ AB=BC,∠A=∠C=90°.由折叠性质,得 BM=AB,∠BMP=∠A=90°.
∴ ∠BMQ=∠C=90°,BM=BC,
∵ BQ=BQ,
∴ Rt△MBQ≌Rt△CBQ(HL).
∴ ∠MBQ=∠CBQ.
(3)$\frac{40}{11}$cm或$\frac{24}{13}$cm