《2025年复习计划风向标暑八年级数学北师大版》

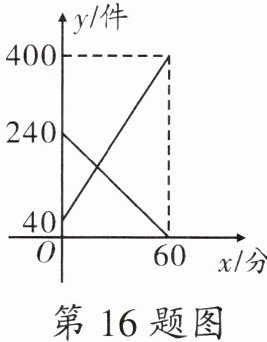
16. 某快递公司每天上午$9:00 - 10:00$为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量$y$(件)与时间$x$(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )

A.$9:15$
B.$9:20$
C.$9:25$
D.$9:30$

答案： B

17. 某苹果种植合作社通过网络销售苹果,如图中线段$AB为苹果日销售量y$(千克)与苹果售价$x$(元/千克)的函数图象的一部分.已知 1 千克苹果的成本价为 5 元,如果某天以 8 元/千克的价格销售苹果,那么这天销售苹果的盈利是______元.

答案： 6600

18. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多 15 元,王老师从该网店购买了 2 筒甲种羽毛球和 3 筒乙种羽毛球,共花费 255 元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过 8780 元购进甲、乙两种羽毛球共 200 筒,且甲种羽毛球的数量大于乙种羽毛球数量的$\frac{3}{5}$,已知甲种羽毛球每筒的进价为 50 元,乙种羽毛球每筒的进价为 40 元.
①若设购进甲种羽毛球$m$筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润$W$(元)与甲种羽毛球进货量$m$(筒)之间的函数关系式,并说明当$m$为何值时所获利润最大,最大利润是多少?

答案： 解:
(1)设甲种羽毛球每筒的售价为x元,乙种羽毛球每筒的售价为y元,根据题意,得$\left\{\begin{array}{l} x-y=15,\\ 2x+3y=255,\end{array}\right.$解得$\left\{\begin{array}{l} x=60,\\ y=45.\end{array}\right.$答:该网店甲种羽毛球每筒的售价为60元,乙种羽毛球每筒的售价为45元.
(2)①若购进甲种羽毛球m筒,则购进乙种羽毛球(200-m)筒,根据题意,得$\left\{\begin{array}{l} 50m+40(200-m)\leq 8780,\\ m＞\frac{3}{5}(200-m).\end{array}\right.$解得75＜m≤78.
∵m为整数,
∴m的值为76,77,78.
∴进货方案有3种:方案一,购进甲种羽毛球76筒,乙种羽毛球124筒;方案二,购进甲种羽毛球77筒,乙种羽毛球123筒;方案三,购进甲种羽毛球78筒,乙种羽毛球122筒. ②根据题意可得$ W=(60-50)m+(45-40)(200-m)=5m+1000 $.
∵5＞0,
∴W随m的增大而增大,且75＜m≤78,
∴当m=78时,W最大,W最大值为1 390.答:当m=78时,所获利润最大,最大利润为1 390元.