2025年复习计划风向标暑八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年复习计划风向标暑八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
15. 如图,在平面直角坐标系中,菱形 $OABC$ 的顶点 $O(0,0)$,$A(4,0)$,$\angle AOC = 60^{\circ}$,则顶点 $B$ 的坐标为______。
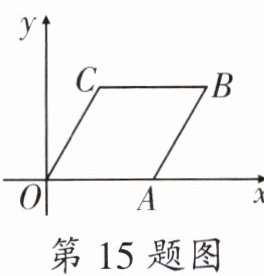

答案:
$(6,2\sqrt{3})$
16. 如图,在菱形 $ABCD$ 中,点 $E$ 在 $BC$ 上,且 $AE = AD$,$\angle EAD = 2\angle BAE$,则 $\angle BAE$ 的度数为______。
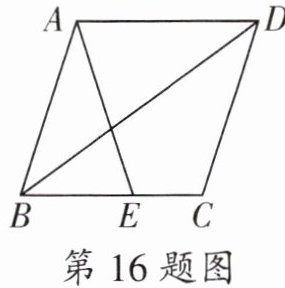

答案:
$36^{\circ}$
17. 如图,菱形 $ABCD$ 的两条对角线的长分别为 $6$ 和 $8$,点 $M$,$N$ 分别是边 $AB$,$BC$ 的中点,点 $P$ 是对角线 $AC$ 上的一个动点,则 $PM + PN$ 的最小值是______。


答案:
5
18. 如图,在四边形 $ABCD$ 中,$AB // DC$,$AB = AD$,对角线 $AC$,$BD$ 交于点 $O$,$AC$ 平分 $\angle BAD$,过点 $C$ 作 $CE \perp AB$ 交 $AB$ 延长线于点 $E$,连接 $OE$。
(1) 求证:四边形 $ABCD$ 是菱形;
(2) 若 $OE = 2\sqrt{3}$,$\angle BAD = 60^{\circ}$,求四边形 $ABCD$ 的面积。
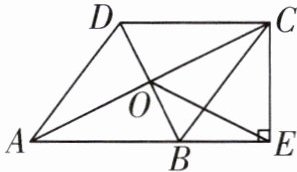
(1) 求证:四边形 $ABCD$ 是菱形;
(2) 若 $OE = 2\sqrt{3}$,$\angle BAD = 60^{\circ}$,求四边形 $ABCD$ 的面积。

答案:
(1)证明:
∵ AB//CD,
∴ ∠OAB =∠DCA.
∵ AC 平分∠BAD,
∴ ∠OAB =∠DAC,
∴ ∠DCA =∠DAC,
∴ CD =AD.
∵ AB =AD,
∴ AB =CD.
∵ AB//CD,
∴ 四边形 ABCD 是平行四边形.
∵ AD =AB,
∴ ▱ABCD 是菱形.
(2)解:
∵ 四边形 ABCD 是菱形,∠BAD =60°,
∴ ∠CAE =30°,∠AOB =90°,AB =2OB,AO =CO.
∴ AO =CO =$\sqrt{AB^{2}-OB^{2}}=\sqrt{3}OB$.
∵ AE⊥CE,即∠AEC =90°,
∴ AC =2CE,OC =OA =OE =$\frac{1}{2}$AC =$2\sqrt{3}$,
∴ OB =2,AC =$4\sqrt{3}$,
∴ BD =4,
∴ $S_{四边形ABCD}=\frac{1}{2}$AC·BD =$8\sqrt{3}$.
(1)证明:
∵ AB//CD,
∴ ∠OAB =∠DCA.
∵ AC 平分∠BAD,
∴ ∠OAB =∠DAC,
∴ ∠DCA =∠DAC,
∴ CD =AD.
∵ AB =AD,
∴ AB =CD.
∵ AB//CD,
∴ 四边形 ABCD 是平行四边形.
∵ AD =AB,
∴ ▱ABCD 是菱形.
(2)解:
∵ 四边形 ABCD 是菱形,∠BAD =60°,
∴ ∠CAE =30°,∠AOB =90°,AB =2OB,AO =CO.
∴ AO =CO =$\sqrt{AB^{2}-OB^{2}}=\sqrt{3}OB$.
∵ AE⊥CE,即∠AEC =90°,
∴ AC =2CE,OC =OA =OE =$\frac{1}{2}$AC =$2\sqrt{3}$,
∴ OB =2,AC =$4\sqrt{3}$,
∴ BD =4,
∴ $S_{四边形ABCD}=\frac{1}{2}$AC·BD =$8\sqrt{3}$.
19. 如图,在正方形 $ABCD$ 外侧作直线 $AP$,点 $B$ 关于直线 $AP$ 的对称点为 $E$,连接 $BE$,$DE$,其中 $DE$ 交直线 $AP$ 于点 $F$,连接 $AE$。若 $\angle PAB = 20^{\circ}$,则 $\angle ADF$ 的度数为______。


答案:
$25^{\circ}$
查看更多完整答案,请扫码查看


