《2025年复习计划风向标暑八年级数学北师大版》

15. (8分)如图,已知在$\triangle ABC$中,$D$,$E$,$F分别是AB$,$BC$,$AC$的中点,连接$DF$,$EF$,$BF$.
(1)求证:四边形$BEFD$是平行四边形;
(2)若$\angle AFB = 90^{\circ}$,$AB = 6$,求四边形$BEFD$的周长.

答案：
(1)证明:
∵ D,E,F 分别是 AB,BC,AC 的中点,
∴ DF//BC,EF//AB,即 DF//BE,EF//BD,
∴ 四边形 BEFD 是平行四边形.
(2)解:
∵ ∠AFB=90°,D 是 AB 的中点,AB=6,
∴ DF=DB=DA=$\frac{1}{2}$AB=3.
∵ 四边形 BEFD 是平行四边形,
∴ 四边形 BEFD 的周长为 2(DB+DF)=2×6=12.

16. (10分)如图,在四边形$ABCD$中,对角线$AC$,$BD相交于点O$,$AO = OC$,$BO = OD$,且$\angle AOB = 2\angle OAD$.
(1)求证:四边形$ABCD$是矩形;
(2)若$\angle AOB:\angle ODC = 4:3$,求$\angle ADO$的度数.

答案：
(1)证明:
∵ AO=OC,BO=OD,
∴ 四边形 ABCD 是平行四边形.
∵ ∠AOB=∠OAD+∠ODA=2∠OAD,
∴ ∠OAD=∠ODA,
∴ AO=DO,
∴ AC=BD,
∴ 四边形 ABCD 是矩形.
(2)解:
∵ 四边形 ABCD 是矩形,
∴ AB//CD,OA=OB,
∴ ∠ABO=∠ODC,∠ABO=∠BAO.
∵ ∠AOB:∠ODC=4:3,
∴ ∠AOB:∠ABO=4:3,
∴ ∠BAO:∠AOB:∠ABO=3:4:3,
∴ ∠ABO=180°×$\frac{3}{3+4+3}$=54°.
∵ ∠BAD=90°,
∴ ∠ADO=90°-54°=36°.

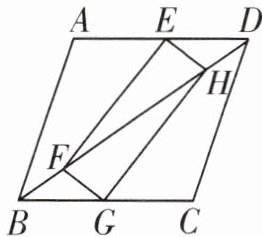
17. (10分)如图,矩形$EFGH的顶点E$,$G分别在菱形ABCD的边AD$,$BC$上,顶点$F$,$H在菱形ABCD的对角线BD$上.
(1)求证:$BG = DE$;
(2)若$E为AD$的中点,$FH = 2$,求菱形$ABCD$的周长.

答案：

(1)证明:
∵ 四边形 EFGH 是矩形,
∴ EH=GF,EH//GF,
∴ ∠GFH=∠EHF.
∵ ∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴ ∠BFG=∠DHE.
∵ 四边形 ABCD 是菱形,
∴ AD//BC,
∴ ∠GBF=∠EDH,
∴ △BGF≌△DEH(AAS),
∴ BG=DE.
(2)解:如图,连接 EG.
∵ 四边形 ABCD 是菱形,
∴ AD=BC,AD//BC.
∵ E 为 AD 的中点,
∴ AE=ED.
∵ BG=DE,
∴ AE=BG.又
∵ AE//BG,
∴ 四边形 ABGE 是平行四边形,
∴ AB=EG.
∵ 四边形 EFGH 是矩形,
∴ EG=FH,
∴ AB=FH.
∵ FH=2,
∴ AB=2,
∴ 菱形 ABCD 的周长为 4AB=8.