《2025年暑假大串联七年级数学浙教版》

例1 若$|a|=3$，$|b|=2$，且$a＞b$，求$a+b$的值。
【解析】：根据绝对值的定义，已知$\vert a\vert =3$，则$a$的值为$3$或$-3$；已知$\vert b\vert =2$，则$b$的值为$2$或$-2$。又因为$a\gt b$，所以分情况讨论：当$a = 3$时，$b$可以取$2$或$-2$都满足$a\gt b$；当$a = -3$时，无论$b$取$2$还是$-2$，都不满足$a\gt b$，所以舍去$a = -3$这种情况。然后分别计算$a = 3$，$b = 2$和$a = 3$，$b = -2$时$a + b$的值。
【答案】：5或1

答案： 【解析】：根据绝对值的定义，已知$\vert a\vert =3$，则$a$的值为$3$或$-3$；已知$\vert b\vert =2$，则$b$的值为$2$或$-2$。又因为$a\gt b$，所以分情况讨论：当$a = 3$时，$b$可以取$2$或$-2$都满足$a\gt b$；当$a = -3$时，无论$b$取$2$还是$-2$，都不满足$a\gt b$，所以舍去$a = -3$这种情况。然后分别计算$a = 3$，$b = 2$和$a = 3$，$b = -2$时$a + b$的值。
【答案】：$5$或$1$

例2 如图，以直线$m$上的点$A$，$B$，$C$，$D$，$E$，$F$为端点的线段有多少条？

15条

答案： 【解析】：按照以左端点为标准进行分类计数，分别计算出以$A$、$B$、$C$、$D$、$E$为左端点的线段数量，再将其相加。
【答案】：$15$条

例3 若$|a|=3$，$\sqrt{b^2}=5$，则$|a+b|=$2或8。
分析：二次根式$\sqrt{b^2}$可以化简，转化为$|b|$，与绝对值有关的问题，一般要去掉绝对值符号，这就要根据绝对值的概念进行分类讨论研究。

答案： 解：$\sqrt{b^2}=|b|$，$a=\pm 3$，$b=\pm 5$。
当$a=3$，$b=5$时，$|a+b|=8$；
当$a=-3$，$b=-5$时，$|a+b|=8$；
当$a=-3$，$b=5$时，$|a+b|=2$；
当$a=3$，$b=-5$时，$|a+b|=2$；
综上所述，$|a+b|=2$或$8$。
故答案为$2$或$8$。

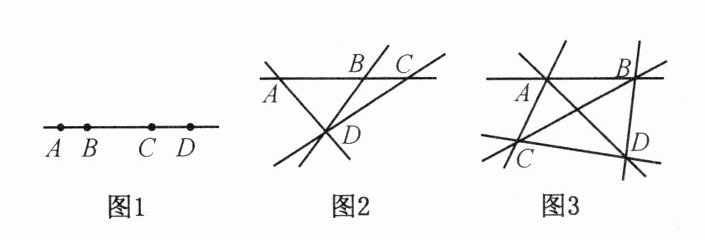
例4 在平面内有四个点$A$，$B$，$C$，$D$，能确定多少条直线？

答案：
【解析】：分三种情况讨论平面内四个点$A$，$B$，$C$，$D$确定直线的数量，分别是四个点在同一直线、三个点在同一直线另一点在外、任意三点都不在同一直线。
【答案】：$1$条或$4$条或$6$条