《2025年暑假大串联七年级数学浙教版》

9. 先阅读下面例题的解题过程,再完成后面的题目.
例:已知$9-6y-4y^{2}=7$,求$2y^{2}+3y+7$的值.
解:由$9-6y-4y^{2}=7$,得$-6y-4y^{2}=7-9$,即$6y+4y^{2}=2$,所以$2y^{2}+3y=1$,所以$2y^{2}+3y+7=8$.
题目:已知代数式$14x+5-21x^{2}$的值是-2,求$6x^{2}-4x+5$的值.
解: $\because 14 x + 5 - 21 x ^ { 2 } = - 2 $, $ \therefore 14 x - 21 x ^ { 2 } = - 7 $, 即 $ 2 x - 3 x ^ { 2 } = - 1 $, $ \therefore 3 x ^ { 2 } - 2 x = 1 $, 则 $ 6 x ^ { 2 } - 4 x + 5 = 2 × (3 x ^ { 2 } - 2 x) + 5 = $7.

答案： 解: $ \because 14 x + 5 - 21 x ^ { 2 } = - 2 $, $ \therefore 14 x - 21 x ^ { 2 } = - 7 $, 即 $ 2 x - 3 x ^ { 2 } = - 1 $, $ \therefore 3 x ^ { 2 } - 2 x = 1 $, 则 $ 6 x ^ { 2 } - 4 x + 5 = 2 × (3 x ^ { 2 } - 2 x) + 5 = 7 $.

10. 小颖做一道数学题“已知两个多项式A,B,其中B为$4x^{2}-5x-6$,求$A+B$”时,错把“$A+B$”看成“$A-B$”,结果求出的答案是$-7x^{2}+10x+12$,那么$A+B$的正确答案应是多少?

答案： 解: 由 $ A - B = - 7 x ^ { 2 } + 10 x + 12 $, 得 $ A = - 7 x ^ { 2 } + 10 x + 12 + B = - 7 x ^ { 2 } + 10 x + 12 + 4 x ^ { 2 } - 5 x - 6 = - 3 x ^ { 2 } + 5 x + 6 $, 所以 $ A + B = - 3 x ^ { 2 } + 5 x + 6 + 4 x ^ { 2 } - 5 x - 6 = x ^ { 2 } $.

1. (恩施中考题)某班共有x个学生,其中女生人数占45%,用式子表示该班的男生人数是0.55x.

答案： $ 0.55 x $

2. (株洲中考题)孔明同学买铅笔m支,每支0.4元,买练习本n本,每本2元,那么他买铅笔和练习本一共花了(0.4m + 2n)元.

答案： $ (0.4 m + 2 n) $

3. (安徽中考题)定义运算$a\otimes b=a(1-b)$,下面给出了关于这种运算的几个结论:
①$2\otimes (-2)=6$
②$a\otimes b=b\otimes a$
③若$a+b=0$,则$(a\otimes a)+(b\otimes b)=2ab$
④若$a\otimes b=0$,则$a=0$
其中正确结论的序号是____①③.

答案： ①③

4. (内江中考题)一个四位数,如果它的千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称该数为“极数”.若偶数m为“极数”,且$\frac{m}{33}$是完全平方数,则$m=$1188 或 4752.

答案： 1188 或 4752

5. (北海中考题)下列式子按一定规律排列:$\frac{a}{2}$,$\frac{a^{3}}{4}$,$\frac{a^{5}}{6}$,$\frac{a^{7}}{8}$,…则第2014个式子是$\frac{a^{4027}}{4028}$.

答案： $ \frac { a ^ { 4027 } } { 4028 } $

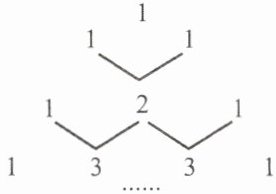
6. (巴中中考题)如图是我国古代数学家杨辉最早发现的,称为“杨辉三角形”.它的出现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角形”中有许多规律,如它的每一行数字正好对应了$(a+b)^{n}$(n为自然数)的展开式中a按次数从大到小排列的项的系数,例如$(a+b)^{2}=a^{2}+2ab+b^{2}$展开式中的系数1,2,1恰好对应图中第三行的数字;再如$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$展开式中的系数1,3,3,1恰好对应图中第四行的数字.请认真观察此图,写出$(a+b)^{4}$的展开式为____$ a ^ { 4 } + 4 a ^ { 3 } b + 6 a ^ { 2 } b ^ { 2 } + 4 a b ^ { 3 } + b ^ { 4 } $.

答案： $ a ^ { 4 } + 4 a ^ { 3 } b + 6 a ^ { 2 } b ^ { 2 } + 4 a b ^ { 3 } + b ^ { 4 } $