2025年暑假大串联七年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假大串联七年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. (包头中考题)如图,已知∠1=∠2,∠3=73°,则∠4的度数为

107
度.
答案:
107
2. (无锡中考题)如图,AB//CD,则根据图中标注的角,下列关系中成立的是 (

A. ∠1=∠3
B. ∠2+∠3=180°
C. ∠2+∠4<180°
D. ∠3+∠5=180°
D
)
A. ∠1=∠3
B. ∠2+∠3=180°
C. ∠2+∠4<180°
D. ∠3+∠5=180°
答案:
D
3. (南通中考题)如图,∠1=40°,如果CD//BE,那么∠B的度数为 (

A. 160°
B. 140°
C. 60°
D. 50°
B
)
A. 160°
B. 140°
C. 60°
D. 50°
答案:
B
4. (滨州中考题)如图是我们学过的用直尺画平行线的方法示意图,画图原理是 (
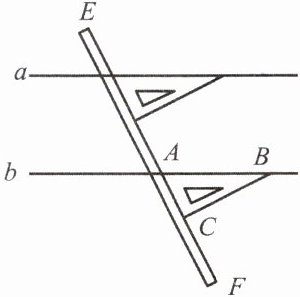
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 两直线平行,同位角相等
D. 两直线平行,内错角相等
A
)
A. 同位角相等,两直线平行
B. 内错角相等,两直线平行
C. 两直线平行,同位角相等
D. 两直线平行,内错角相等
答案:
A
5. (梅州中考题)如图,把一块含有45°角的直角三角板两个顶点放在直尺的对边上,如果∠1=20°,则∠2的度数是 (

A. 15°
B. 20°
C. 25°
D. 30°
C
)
A. 15°
B. 20°
C. 25°
D. 30°
答案:
C
6. (赤峰中考题)如图甲,E是直线AB,CD内部一点,AB//CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于
②若∠A=20°,∠D=60°,则∠AED等于
③猜想图甲中∠AED,∠A,∠D的关系并证明你的结论.
(2)拓展应用:
如图乙,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③④位于直线AB上方),P是位于以上四个区域上的点,猜想∠PEB,∠PFC,∠EPF的关系.(不要求证明)
当点P在区域①时,
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于
70°
.②若∠A=20°,∠D=60°,则∠AED等于
80°
.③猜想图甲中∠AED,∠A,∠D的关系并证明你的结论.
∠AED=∠A+∠D
(2)拓展应用:
如图乙,射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③④位于直线AB上方),P是位于以上四个区域上的点,猜想∠PEB,∠PFC,∠EPF的关系.(不要求证明)
当点P在区域①时,
∠PEB+∠PFC+∠EPF=360°
;当点P在区域②时,∠EPF=∠PEB+∠PFC
;当点P在区域③时,∠PEB=∠PFC+∠EPF
;当点P在区域④时,∠PFC=∠PEB+∠EPF
.
答案:
(1)①$70^{\circ}$ ②$80^{\circ}$ ③$\angle AED=\angle A+\angle D$,证明略。
(2)当点P在区域①时,$\angle PEB+\angle PFC+\angle EPF=360^{\circ}$;
当点P在区域②时,$\angle EPF=\angle PEB+\angle PFC$;
当点P在区域③时,$\angle PEB=\angle PFC+\angle EPF$;
当点P在区域④时,$\angle PFC=\angle PEB+\angle EPF$。
(1)①$70^{\circ}$ ②$80^{\circ}$ ③$\angle AED=\angle A+\angle D$,证明略。
(2)当点P在区域①时,$\angle PEB+\angle PFC+\angle EPF=360^{\circ}$;
当点P在区域②时,$\angle EPF=\angle PEB+\angle PFC$;
当点P在区域③时,$\angle PEB=\angle PFC+\angle EPF$;
当点P在区域④时,$\angle PFC=\angle PEB+\angle EPF$。
查看更多完整答案,请扫码查看


