《2025年暑假大串联七年级数学浙教版》

15. 某校运动员按规定组数进行分组训练，若每组$7$人，余$3$人；若每组$8$人，则缺$5$人.设运动员人数为$x$人，组数为$y$组，则可列出的方程组为（D）
A. $\left\{\begin{array}{l} 7y=x+3\\ 8y=x-5\end{array}\right. $
B. $\left\{\begin{array}{l} 7y=x+3\\ 8y=x+5\end{array}\right. $
C. $\left\{\begin{array}{l} 7y=x-3\\ 8y=x-5\end{array}\right. $
D. $\left\{\begin{array}{l} 7y=x-3\\ 8y=x+5\end{array}\right. $

答案： D

16. 计算：
（1）$(x+2)^{2}-(x+1)(x-1)$
（2）$(1+\frac {1}{x-1})÷\frac {x}{x^{2}-1}$

答案：
(1) $ 4x + 5 $
(2) $ x + 1 $

17. 因式分解：
（1）$4a^{3}-8a^{2}+4a$
（2）$x^{3}-xy^{2}$

答案：
(1) $ 4a(a - 1)^2 $
(2) $ x(x + y)(x - y) $

18. 解方程（组）：
（1）$\left\{\begin{array}{l} 2x-y=5\\ 3x+2y=4\end{array}\right. $
解：$\begin{cases} x = 2 \\ y = -1 \end{cases}$
（2）$\frac {2}{1-x}+1=\frac {x}{1+x}$
解：$x = -3$

答案：
(1) $ \begin{cases} x = 2 \\ y = -1 \end{cases} $
(2) $ x = -3 $

19. 先化简，再求值：$(x+1)÷(2+\frac {1+x^{2}}{x})$，其中$x=-\frac {3}{2}$.

答案： 解：原式 $ = (x + 1) ÷ \frac{2x + 1 + x^2}{x} = (x + 1) \cdot \frac{x}{(x + 1)^2} = \frac{x}{x + 1} $
当 $ x = -\frac{3}{2} $ 时，原式 $ = \frac{-\frac{3}{2}}{-\frac{3}{2} + 1} = 3 $。

20. 某市园林处去年植树节在滨海路两侧栽了$A$，$B$，$C$三个品种的树苗.栽种的$A$，$B$，$C$三个品种树苗数量的扇形统计图如图$1$所示，其中$B$种树苗数量对应的扇形圆心角为$120^{\circ }$.今年植树节前管理员调查了这三个品种树苗的成活率情况，准备今年从三个品种中选成活率最高的品种再进行栽种.经调查得知：$A$品种的成活率为$85\%$，三个品种的总成活率为$89\%$，但三个品种树苗成活数量统计图尚不完整，如图$2$所示.
请你根据以上信息帮管理员解决下列问题：
（1）三个品种树苗去年共栽多少棵？
（2）补全条形统计图，并通过计算，说明今年应栽哪个品种的树苗？

答案：
解：
(1) $ A $ 品种树苗棵数为 $ 1020 ÷ 85\% = 1200 $（棵），
所以三个品种树苗共栽棵数为 $ 1200 ÷ 40\% = 3000 $（棵）。
(2) $ B $ 品种树苗成活棵数为 $ 3000 × 89\% - 1020 - 720 = 930 $（棵）。补全条形统计图如图所示:

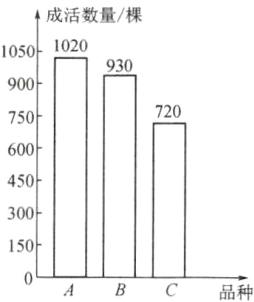
$ B $ 品种树苗成活率为 $ \frac{930}{3000 × \frac{120}{360}} × 100\% = 93\% $；
$ C $ 品种树苗成活率为 $ \frac{720}{3000 - 1200 - 3000 × \frac{120}{360}} × 100\% = 90\% $。
所以，$ B $ 品种成活率最高，今年应栽 $ B $ 品种树苗。