《2025年金钥匙课时学案作业本九年级数学上册人教版》

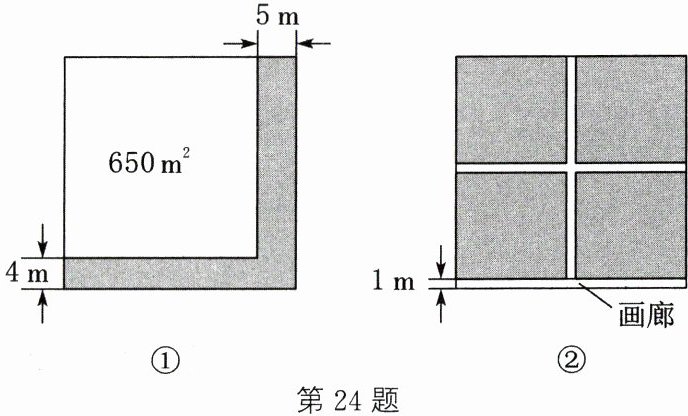
24. (10分)如图①,某校进行校园改造,准备将一块正方形空地划出一部分用于栽种鲜花,原空地一边减少了4m,另一边减少了5m,剩余部分的面积为$650m^{2}$.
(1) 求原正方形空地的边长.
(2) 实际改造时,该校从美观和实用的角度考虑,按如图②所示的方式进行改造,先在正方形空地的一侧建成1m宽的画廊,再在余下部分建成宽度相等的两条小道,其余部分栽种鲜花.若栽种鲜花部分的面积为$812m^{2}$,求小道的宽度.

答案：
(1) 设原正方形空地的边长为 $ x $ m，根据题意得：
$(x - 4)(x - 5) = 650$
展开并整理：$x^2 - 9x - 630 = 0$
解得：$x_1 = 30$，$x_2 = -21$（舍去）
答：原正方形空地的边长为 30 m。
(2) 设小道的宽度为 $ y $ m，画廊宽 1 m，剩余部分长为 $ 30 - 1 = 29 $ m，宽为 30 m。
根据题意得：$(29 - y)(30 - y) = 812$
展开并整理：$y^2 - 59y + 58 = 0$
解得：$y_1 = 1$，$y_2 = 58$（舍去）
答：小道的宽度为 1 m。