《2025年金钥匙课时学案作业本九年级数学上册人教版》

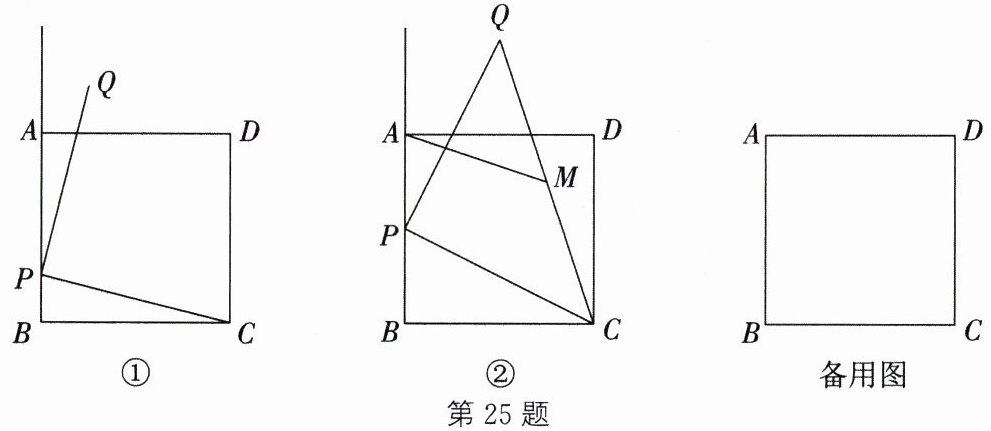
25. (13分)已知正方形$ABCD$的边长为4,$P为边AB$上一点,连接$CP$,将线段$PC绕点P逆时针旋转90^{\circ}$,得到线段$PQ$.
(1) 如图①,当$BP= 1$时,求点$Q到直线AB$的距离.
(2) 如图②,连接$CQ$,取$CQ的中点M$,连接$AM$.求证:$AM= \frac{1}{2}CQ$.
(3) 连接$QA,QD$.当$\triangle ADQ$为等腰三角形时,求$BP$的长.

答案：
(1) 解：过点Q作QE⊥AB交AB延长线于E，
∵∠QPE+∠BPC=90°，∠BPC+∠BCP=90°，
∴∠QPE=∠BCP，
又
∵PQ=PC，∠QEP=∠PBC=90°，
∴△QEP≌△PBC(AAS)，
∴QE=BP=1，
即点Q到直线AB的距离为1。
(2) 证明：延长AM至N，使MN=AM，连接CN，
∵M为CQ中点，
∴QM=CM，
又∠QMA=∠CMN，
∴△QMA≌△CMN(SAS)，
∴AQ=CN，∠MAQ=∠N，
∴AQ//CN，
∵∠QAD+∠DCN=180°，∠DAB=90°，
∴∠BAQ=∠NCD，
又AB=CD，AQ=CN，
∴△ABQ≌△CDN(SAS)，
∴BQ=DN，∠ABQ=∠CDN，
∵∠ADQ+∠CDN=90°，
∴∠ADQ+∠ABQ=90°，
又∠ABQ=∠DAQ，
∴∠DAQ+∠ADQ=90°，
∴∠AQD=90°，在Rt△AQC中，M为CQ中点，
∴AM=1/2CQ。
(3) 解：设BP=x，则AP=4-x，
由
(1)知QE=x，PE=BC=4，
∴Q(-x, 4-x)，
A(0,4)，D(4,4)，
AD=4，AQ=√(x²+x²)=√2|x|，DQ=√((x+4)²+x²)，
①AQ=AD：√2x=4→x=2√2；
②AQ=DQ：√2x=√((x+4)²+x²)→x=4+4√2(舍)或x=4-4√2(舍)；
③AD=DQ：√((x+4)²+x²)=4→x=0或x=-4(舍)，
综上，BP=2√2或0。
答案：
(1)1；
(2)见解析；
(3)0或2√2。