《2025年金钥匙课时学案作业本九年级数学上册人教版》

22. (10分)如图,在$\triangle ABC$中,$AB= AC$,$\angle BAC= 42^{\circ}$,$D为\triangle ABC$内一点,连接$AD$,将线段$AD绕点A逆时针旋转42^{\circ}后得到线段AE$,连接$DE$,$BD$,$CE$.
(1) 求证:$BD= CE$;
(2) 若$DE\perp AC$,求$\angle BAD$的度数.

答案：
(1) 证明：
∵AB=AC，∠BAC=42°，
∴∠ABC=∠ACB=(180°-42°)/2=69°，
∵线段AD绕点A逆时针旋转42°得到线段AE，
∴AD=AE，∠DAE=42°，
∴∠BAC=∠DAE，
∴∠BAC-∠DAC=∠DAE-∠DAC，
即∠BAD=∠CAE，
在△ABD和△ACE中，
AB=AC，∠BAD=∠CAE，AD=AE，
∴△ABD≌△ACE(SAS)，
∴BD=CE；
(2) 解：
∵AD=AE，∠DAE=42°，
∴∠ADE=∠AED=(180°-42°)/2=69°，
∵DE⊥AC，
∴∠AED+∠CAE=90°，
∴∠CAE=90°-∠AED=90°-69°=21°，
由
(1)知∠BAD=∠CAE，
∴∠BAD=21°。

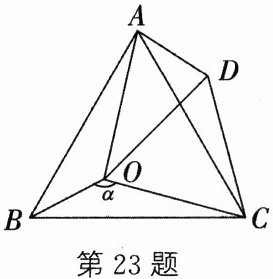
23. (12分)如图,$O是等边三角形ABC$内一点,$\angle AOB= 130^{\circ}$,$\angle BOC= \alpha$.将$\triangle BOC绕点C顺时针旋转60^{\circ}得到\triangle ADC$,连接$OD$.
(1) 判断$\triangle COD$的形状,并加以证明;
(2) 若$AD= 1$,$OC= \sqrt{2}$,$OA= \sqrt{3}$,求$\alpha$的度数;
(3) 当$\alpha$为多少度时,$\triangle AOD$是等腰三角形?

答案：
(1) 解：△COD是等边三角形。
证明：
∵将△BOC绕点C顺时针旋转60°得到△ADC，
∴OC=DC，∠OCD=60°，
∴△COD是等边三角形。
(2) 解：
∵△COD是等边三角形，
∴OD=OC=√2，∠ODC=60°。
∵将△BOC绕点C顺时针旋转60°得到△ADC，
∴AD=BO。
在△AOD中，OA=√3，OD=√2，AD=1，
∵OA²=OD²+AD²，
∴∠ADO=90°，
∵∠ODC=60°，
∴∠ADC=∠ADO+∠ODC=150°，
∵△BOC≌△ADC，
∴∠BOC=∠ADC=150°，即α=150°。
(3) 解：
∵△COD是等边三角形，
∴∠COD=∠CDO=60°。
∵∠AOB=130°，∠BOC=α，
∴∠AOC=360°-∠AOB-∠BOC=360°-130°-α=230°-α。
∵∠AOD=∠AOC-∠COD=230°-α-60°=170°-α。
∵△BOC≌△ADC，
∴∠ADC=∠BOC=α，
∴∠ADO=∠ADC-∠CDO=α-60°。
在△AOD中，∠OAD=180°-∠AOD-∠ADO=180°-(170°-α)-(α-60°)=70°。
① 若AO=AD，则∠AOD=∠ADO，
170°-α=α-60°，解得α=115°；
② 若OA=OD，则∠OAD=∠ADO，
70°=α-60°，解得α=130°；
③ 若OD=AD，则∠OAD=∠AOD，
70°=170°-α，解得α=100°。
综上所述，α=115°或130°或100°。