《2025年金钥匙课时学案作业本九年级数学上册人教版》

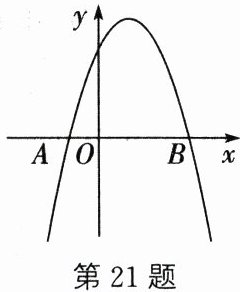
21. (10分)如图,抛物线$y= -x^{2}+bx+c经过A(-1,0)$,$B(3,0)$两点.
(1) 求该抛物线对应的函数解析式和顶点坐标;
(2) 当$0＜x＜3$时,直接写出$y$的取值范围;
(3) 若$P$为抛物线上一点,$S_{\triangle PAB}= 10$,求点$P$的坐标.

答案：
(1)解：
∵抛物线$y=-x^{2}+bx+c$经过$A(-1,0)$，$B(3,0)$，
$\therefore \begin{cases} -(-1)^{2}+b×(-1)+c=0 \\ -(3)^{2}+b×3+c=0 \end{cases}$，
即$\begin{cases} -1 - b + c = 0 \\ -9 + 3b + c = 0 \end{cases}$，
解得$\begin{cases} b = 2 \\ c = 3 \end{cases}$，
$\therefore$抛物线解析式为$y=-x^{2}+2x + 3$，
$\because y=-x^{2}+2x + 3=-(x - 1)^{2}+4$，
$\therefore$顶点坐标为$(1,4)$；
(2)$0 ＜ y \leq 4$；
(3)解：$\because A(-1,0)$，$B(3,0)$，
$\therefore AB=3 - (-1)=4$，
设$P(x,y)$，
$\because S_{\triangle PAB}=10$，
$\therefore \frac{1}{2}× AB×|y|=10$，
即$\frac{1}{2}×4×|y|=10$，
$2|y|=10$，$|y|=5$，$y = \pm5$，
当$y = 5$时，$-x^{2}+2x + 3=5$，
$-x^{2}+2x - 2=0$，$x^{2}-2x + 2=0$，
$\Delta=(-2)^{2}-4×1×2=4 - 8=-4 ＜ 0$，方程无解，
当$y=-5$时，$-x^{2}+2x + 3=-5$，
$-x^{2}+2x + 8=0$，$x^{2}-2x - 8=0$，
$(x - 4)(x + 2)=0$，$x - 4=0$或$x + 2=0$，
解得$x = 4$或$x=-2$，
$\therefore P(4,-5)$或$(-2,-5)$。

22. (10分)已知二次函数$y= ax^{2}-4x+c的图象经过点A(-1,-1)和点B(3,-9)$.
(1) 求该二次函数的解析式;
(2) 求该二次函数图象的对称轴及顶点坐标;
(3) 点$C(m,m)$(其中$m＞0$)与点$D$均在该函数图象上,且这两点关于函数图象的对称轴对称,求$m的值及点D$的坐标.

答案：
(1)解：将点A(-1,-1)和点B(3,-9)代入$y=ax^{2}-4x+c$，得
$\begin{cases}a×(-1)^{2}-4×(-1)+c=-1\\a×3^{2}-4×3+c=-9\end{cases}$
$\begin{cases}a + 4 + c=-1\\9a - 12 + c=-9\end{cases}$
$\begin{cases}a + c=-5\\9a + c=3\end{cases}$
两式相减得：$8a=8$，$a=1$
将$a=1$代入$a + c=-5$，得$c=-6$
所以二次函数解析式为$y=x^{2}-4x - 6$
(2)解：$y=x^{2}-4x - 6=(x - 2)^{2}-10$
对称轴为直线$x=2$，顶点坐标为(2,-10)
(3)解：因为点$C(m,m)$在函数图象上，所以$m=m^{2}-4m - 6$
$m^{2}-5m - 6=0$
$(m - 6)(m + 1)=0$
$m=6$或$m=-1$
因为$m＞0$，所以$m=6$，点$C(6,6)$
对称轴为直线$x=2$，设点$D(x,6)$
则$\frac{6 + x}{2}=2$，$x=-2$
所以点$D$的坐标为(-2,6)