《2025年金钥匙课时学案作业本九年级数学上册人教版》

24. (10分)在正方形$ABCD$中,$F为正方形ABCD$内一点,$\triangle BFC绕点B逆时针旋转90^{\circ}后与\triangle BEA$重合.
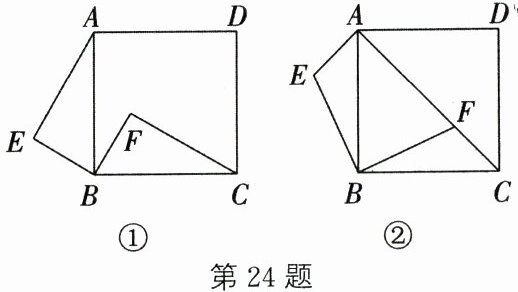
(1) 如图①,若正方形$ABCD$的边长为2,$BE= 1$,$FC= \sqrt{3}$,求证:$AE// BF$;
(2) 如图②,若$F为正方形ABCD的对角线AC$上一点(点$F不与点A$,$C$重合),试探究$AE$,$AF$,$BF$之间的数量关系,并加以证明.

答案：
(1)证明：
∵△BFC绕点B逆时针旋转90°后与△BEA重合，
∴△BFC≌△BEA，∠EBF=90°，
∴BE=BF=1，AE=FC=√3，
在△BEF中，BE²+BF²=1²+1²=2，
在△AEB中，AE²+BE²=(√3)²+1²=4，
∵正方形边长为2，
∴AB=2，AB²=4，
∴AE²+BE²=AB²，
∴∠AEB=90°，
∵∠EBF=90°，
∴∠AEB=∠EBF，
∴AE//BF；
(2)解：AE²+AF²=2BF²，证明如下：
连接EF，
∵△BFC绕点B逆时针旋转90°后与△BEA重合，
∴△BFC≌△BEA，∠EBF=90°，
∴BE=BF，AE=FC，
∴△BEF是等腰直角三角形，
∴EF²=BE²+BF²=2BF²，
∵四边形ABCD是正方形，
∴∠BAC=45°，
∵△BFC≌△BEA，
∴∠BAE=∠BCF=45°，
∴∠EAF=∠BAE+∠BAC=45°+45°=90°，
在Rt△EAF中，AE²+AF²=EF²，
∵EF²=2BF²，
∴AE²+AF²=2BF²。