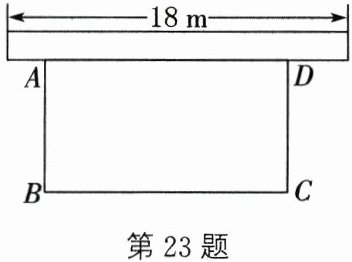
23. (12分)为响应“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过$18m$,另外三边由$36m$长的栅栏围成. 设在矩形空地$ABCD$中,垂直于墙的边$AB= xm$,面积为$y m^{2}$(如图).
(1) 求$y与x$之间的函数解析式,并写出自变量$x$的取值范围.
(2) 若矩形空地的面积为$160m^{2}$,求$x$的值.
(3) 若该单位用$8600$元购买了甲、乙、丙三种绿色植物共$400$棵(每种绿色植物的单价和每棵栽种的合理用地面积如下表),则丙种绿色植物最多可以购买多少棵? 此时,这批绿色植物可以全部栽种到这块空地上吗?
| 绿色植物种类 | 甲 | 乙 | 丙 |
| :---: | :---: | :---: | :---: |
| 单价/(元/棵) | $14$ | $16$ | $28$ |
| 每棵合理用地面积/$m^{2}$ | $0.4$ | $1$ | $0.4$ |
(1) 求$y与x$之间的函数解析式,并写出自变量$x$的取值范围.
(2) 若矩形空地的面积为$160m^{2}$,求$x$的值.
(3) 若该单位用$8600$元购买了甲、乙、丙三种绿色植物共$400$棵(每种绿色植物的单价和每棵栽种的合理用地面积如下表),则丙种绿色植物最多可以购买多少棵? 此时,这批绿色植物可以全部栽种到这块空地上吗?
| 绿色植物种类 | 甲 | 乙 | 丙 |
| :---: | :---: | :---: | :---: |
| 单价/(元/棵) | $14$ | $16$ | $28$ |
| 每棵合理用地面积/$m^{2}$ | $0.4$ | $1$ | $0.4$ |

答案:
(1) 解:因为垂直于墙的边$AB = xm$,另外三边栅栏长$36m$,所以平行于墙的边$BC=(36 - 2x)m$。面积$y = AB×BC = x(36 - 2x)=-2x^{2}+36x$。
由墙长不超过$18m$,得$36 - 2x\leqslant18$,解得$x\geqslant9$;又因为$36 - 2x>0$,得$x<18$,所以自变量$x$的取值范围是$9\leqslant x<18$。
(2) 解:当$y = 160$时,$-2x^{2}+36x = 160$,即$x^{2}-18x + 80 = 0$,解得$x_{1}=8$,$x_{2}=10$。因为$9\leqslant x<18$,所以$x = 10$。
(3) 解:设购买丙种绿色植物$m$棵,甲种$n$棵,则乙种$(400 - m - n)$棵。
由费用得$14n + 16(400 - m - n)+28m = 8600$,化简得$n = 10m - 150$。
因为$n\geqslant0$,$400 - m - n\geqslant0$,所以$\begin{cases}10m - 150\geqslant0\\400 - m-(10m - 150)\geqslant0\end{cases}$,解得$15\leqslant m\leqslant50$,所以丙种最多购买$50$棵。
此时$n = 10×50 - 150 = 350$,乙种$400 - 50 - 350 = 0$棵。
所需面积:$350×0.4 + 0×1 + 50×0.4 = 160m^{2}$。
由
(1)知$y=-2x^{2}+36x$,当$x = 9$时,$y_{max}=-2×81 + 324 = 162m^{2}$,$160\leqslant162$,可以全部栽种。
答:
(1)$y=-2x^{2}+36x(9\leqslant x<18)$;
(2)$x = 10$;
(3)丙种最多购买$50$棵,能全部栽种。
(1) 解:因为垂直于墙的边$AB = xm$,另外三边栅栏长$36m$,所以平行于墙的边$BC=(36 - 2x)m$。面积$y = AB×BC = x(36 - 2x)=-2x^{2}+36x$。
由墙长不超过$18m$,得$36 - 2x\leqslant18$,解得$x\geqslant9$;又因为$36 - 2x>0$,得$x<18$,所以自变量$x$的取值范围是$9\leqslant x<18$。
(2) 解:当$y = 160$时,$-2x^{2}+36x = 160$,即$x^{2}-18x + 80 = 0$,解得$x_{1}=8$,$x_{2}=10$。因为$9\leqslant x<18$,所以$x = 10$。
(3) 解:设购买丙种绿色植物$m$棵,甲种$n$棵,则乙种$(400 - m - n)$棵。
由费用得$14n + 16(400 - m - n)+28m = 8600$,化简得$n = 10m - 150$。
因为$n\geqslant0$,$400 - m - n\geqslant0$,所以$\begin{cases}10m - 150\geqslant0\\400 - m-(10m - 150)\geqslant0\end{cases}$,解得$15\leqslant m\leqslant50$,所以丙种最多购买$50$棵。
此时$n = 10×50 - 150 = 350$,乙种$400 - 50 - 350 = 0$棵。
所需面积:$350×0.4 + 0×1 + 50×0.4 = 160m^{2}$。
由
(1)知$y=-2x^{2}+36x$,当$x = 9$时,$y_{max}=-2×81 + 324 = 162m^{2}$,$160\leqslant162$,可以全部栽种。
答:
(1)$y=-2x^{2}+36x(9\leqslant x<18)$;
(2)$x = 10$;
(3)丙种最多购买$50$棵,能全部栽种。
查看更多完整答案,请扫码查看


