《2025年金钥匙课时学案作业本九年级数学上册人教版》

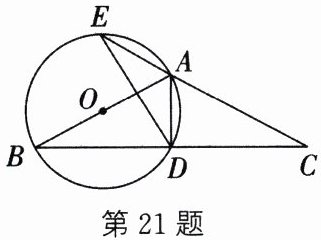
21. (10分)如图,在$\triangle ABC$中,$AB= AC$,以AB为直径作$\odot O$,交边BC于点D,交CA的延长线于点E,连接AD,DE.
(1) 求证:D是边BC的中点;
(2) 若$DE= 4,AD= 2$,求$\odot O$的半径.

答案： 【解析】：
(1)证明：连接$AD$，
∵$AB$为$\odot O$的直径，
∴$\angle ADB=90^\circ$（直径所对的圆周角是直角），
∴$AD\perp BC$，
∵$AB=AC$，
∴$D$是边$BC$的中点（等腰三角形三线合一）。
(2)
∵$AB=AC$，
∴$\angle ABC=\angle C$，
∵四边形$ABDE$是圆内接四边形，
∴$\angle EDC=\angle ABC$（圆内接四边形的一个外角等于它的内对角），
∴$\angle EDC=\angle C$，
∴$ED=EC$，
∵$DE=4$，
∴$EC=4$，
∵$\angle EDA=\angle ABC$，$\angle ABC=\angle ACB$，$\angle ACB=\angle DCE$，
∴$\angle EDA=\angle DCE$，
∵$\angle E=\angle E$，
∴$\triangle EAD\sim \triangle EDC$（两角对应相等的三角形相似），
∴$\frac{EA}{ED}=\frac{ED}{EC}$，
∴$EA=\frac{ED^2}{EC}=\frac{4^2}{4}=4$，
∴$AC=EA+EC=8$，
∵$\angle ADB=90^\circ$，
∴$AC^2=AD^2+CD^2$，
∴$8^2=2^2+CD^2$，
∴$CD=2\sqrt{15}$，
∴$BD=CD=2\sqrt{15}$，
∵$AB^2=AD^2+BD^2$，
∴$AB=\sqrt{2^2+(2\sqrt{15})^2}=4\sqrt{10}$，
∴$\odot O$的半径为$\frac{AB}{2}=2\sqrt{10}$。
【答案】：
(1)证明：连接$AD$，
∵$AB$为$\odot O$的直径，
∴$\angle ADB=90^\circ$，
∴$AD\perp BC$，
∵$AB=AC$，
∴$D$是边$BC$的中点。
(2)$2\sqrt{10}$。

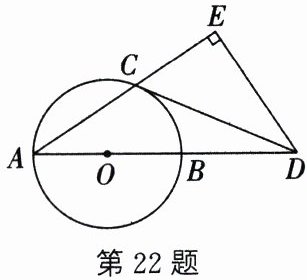
22. (10分)如图,AB是$\odot O$的直径,点C在$\odot O$上,点D,E分别在AB,AC的延长线上,$DE⊥AE$,垂足为E,CD与$\odot O$相切于点C.
(1) 求证:$∠A= ∠CDE$;
(2) 若$AB= 4,BD= 3$,求CD的长.

答案：
(1)证明：连接OC，
∵CD与$\odot O$相切于点C，
∴OC⊥CD，即∠OCD=90°，
∵DE⊥AE，
∴∠E=90°，
∵OA=OC，
∴∠A=∠OCA，
∵∠OCA+∠ECD=90°，∠CDE+∠ECD=90°，
∴∠OCA=∠CDE，
∴∠A=∠CDE；
(2)解：
∵AB=4，
∴OA=OB=OC=2，
∵BD=3，
∴OD=OB+BD=2+3=5，
在Rt△OCD中，OC²+CD²=OD²，
即2²+CD²=5²，
解得CD=$\sqrt{21}$．