17. 如图,在$□ ABCD$中,以点A为圆心,AB为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与$\odot A$相交于点F.若$\widehat {EF}的长为\frac {π}{2}$,则阴影部分的面积为______
$2-\frac{\pi}{2}$
.
答案:
答案为$2-\frac{\pi}{2}$。
答案为$2-\frac{\pi}{2}$。
18. 如图,在$\triangle ABC$中,$∠B= 45^{\circ },∠ACB= 75^{\circ },AB= 4$,D是边BC上的一个动点,以AD为直径画$\odot O$,分别交AB,AC于点E,F,连接EF,则EF长的最小值为______.
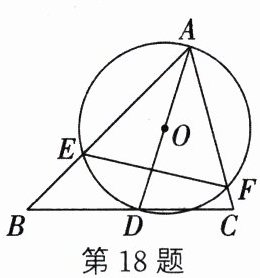

答案:
$\sqrt{6}$
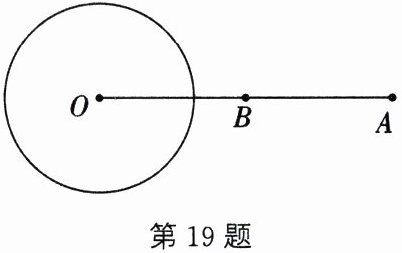
19. (10分)已知A是$\odot O$外一点,B是线段OA的中点.
(1) 如图,过点A作$\odot O$的一条切线,切点为C(要求:尺规作图,保留作图痕迹);
(2) 在(1)的条件下,若$AC= \sqrt {3}AB$,求证:点B在$\odot O$上.
(1) 如图,过点A作$\odot O$的一条切线,切点为C(要求:尺规作图,保留作图痕迹);
(2) 在(1)的条件下,若$AC= \sqrt {3}AB$,求证:点B在$\odot O$上.

答案:
(1)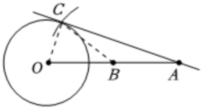
(2) 证明:连接OC。
∵AC是$\odot O$切线,
∴$OC\perp AC$,$\angle OCA=90°$。
设$AB=x$,则$AC=\sqrt{3}x$。
∵B是OA中点,
∴$OA=2AB=2x$。
在$Rt\triangle OAC$中,$OC^2+AC^2=OA^2$,
即$OC^2+(\sqrt{3}x)^2=(2x)^2$,
$OC^2+3x^2=4x^2$,
$OC^2=x^2$,
$OC=x$。
∵$OB=AB=x$,
∴$OB=OC$。
∴点B在$\odot O$上。
(1)

(2) 证明:连接OC。
∵AC是$\odot O$切线,
∴$OC\perp AC$,$\angle OCA=90°$。
设$AB=x$,则$AC=\sqrt{3}x$。
∵B是OA中点,
∴$OA=2AB=2x$。
在$Rt\triangle OAC$中,$OC^2+AC^2=OA^2$,
即$OC^2+(\sqrt{3}x)^2=(2x)^2$,
$OC^2+3x^2=4x^2$,
$OC^2=x^2$,
$OC=x$。
∵$OB=AB=x$,
∴$OB=OC$。
∴点B在$\odot O$上。
20. (10分)已知$\odot O$的半径OA垂直于弦BC,点D在$\odot O$上(不与点A,B,C重合),$∠AOC= 70^{\circ }$.
(1) 如图,当点D在优弧BC上时,求$∠ADB$的度数;
(2) 若点D在劣弧BC上,请直接写出$∠ADB$的度数.

(1) 如图,当点D在优弧BC上时,求$∠ADB$的度数;
(2) 若点D在劣弧BC上,请直接写出$∠ADB$的度数.

答案:
(1) 解:
∵OA垂直于弦BC,
∴弧AB=弧AC,
∵∠AOC=70°,
∴∠AOB=∠AOC=70°,
∴∠BOC=∠AOB+∠AOC=140°,
∵点D在优弧BC上,
∴∠ADB=$\frac{1}{2}$∠AOB=35°;
(2) 145°
(1) 解:
∵OA垂直于弦BC,
∴弧AB=弧AC,
∵∠AOC=70°,
∴∠AOB=∠AOC=70°,
∴∠BOC=∠AOB+∠AOC=140°,
∵点D在优弧BC上,
∴∠ADB=$\frac{1}{2}$∠AOB=35°;
(2) 145°
查看更多完整答案,请扫码查看


