2025年考前示范卷九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年考前示范卷九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
26.(10分)如图1,在△ABC中,AB = AC = 15,BC = 24,点P以每秒1个单位长度的速度,从点A出发沿AB方向向终点B运动,同时,点Q以每秒2个单位长度的速度,从点B出发沿BC方向向终点C运动,当其中一个点到达终点时,另一个点也随之停止运动。设运动时间为ts,请解答下列问题:
(1)当t为何值时,PQ//AC?
(2)在点P,Q的运动过程中,是否存在某一时刻t,使得△PCQ的面积为6?若存在,请求出t的值;若不存在,请说明理由;
(3)如图2,E是AC的中点,S△ABC = 2S△ABE,连接BE,与PQ交于点O,是否存在某一时刻t,使得PQ⊥BE?若存在,请求出t的值;若不存在,请说明理由。
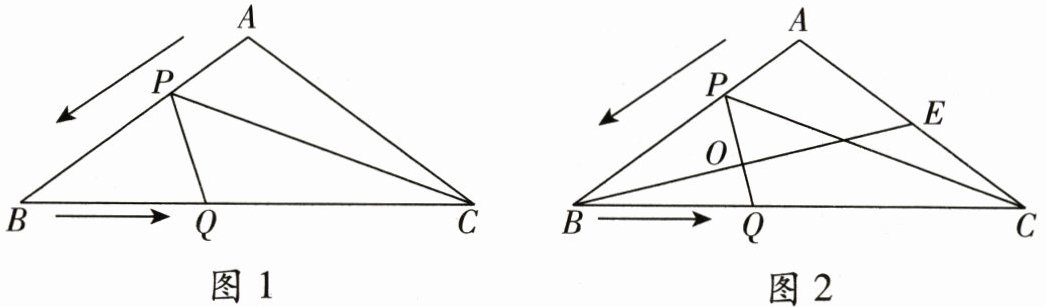
(1)当t为何值时,PQ//AC?
(2)在点P,Q的运动过程中,是否存在某一时刻t,使得△PCQ的面积为6?若存在,请求出t的值;若不存在,请说明理由;
(3)如图2,E是AC的中点,S△ABC = 2S△ABE,连接BE,与PQ交于点O,是否存在某一时刻t,使得PQ⊥BE?若存在,请求出t的值;若不存在,请说明理由。

答案:
解:
(1)由题意,得AP=t,BQ=2t。
∴BP=15−t,CQ=24−2t。
∵点P以每秒1个单位长度的速度由点A出发沿AB方向向点B移动,亠:.当点P由点A移动到点B时,所用时间为tA=15÷1=15(s)。
∵点Q以每秒2个单位长度的速度由点B出发沿
BC方向向点C移动,
∴当点Q由点B移动到点C时,所用时间为tB=24÷2=12(s)。
∵当点P或点Q任意一点到达终点时,另一点停止移动,
∴运动时间t的取值范围为0<t≤12。
∵PQ//AC,
∴$\frac{BP}{AB}$=$\frac{BQ}{BC}$,即$\frac{15−t}{15}$=$\frac{2t}{24}$。
解得t=$\frac{20}{3}$。
∴当t=$\frac{20}{3}$时,PQ//AC。
(2)存在某一时刻t,使得△PCQ的面积为6。理由如下:
如图1,过点A作AF⊥BC于点F,过点P作PH⊥BC于点H。

∴AF//PH。
∴△BPH∽△BAF。
∴$\frac{PH}{AF}$=$\frac{BP}{BA}$。
∴.AB=AC,AF⊥BC,BC=24,
.BF=CF=$\frac{1}{2}$BC=12。
在Rt△ABF中,AB=15,BF=12,
= $\sqrt{AB²−BF²}$= $\sqrt{15²−122}$=9。
彐 15−t
“15°
.,PI=9−3o
.,PI.S△PCQ=6,
1C ,即$\frac{1}{2}$(24−2t)(9−)=66
t7。
<t
∴t=10。
∴当t=10时,△PCQ的面积为6。
(3)存在某一时刻t,使得PQ⊥BE。
如图2,过点A作AF⊥BC于点F,作AM⊥BE,交BE于点K,交BC于点M,过点E作EN⊥BC 于点N。

∴EN//AF。
由
(2),知AF=9,BF=CF=12,
∵E是AC的中点,AC=15,
∴AE=EC=$\frac{1}{2}$C=$\frac{15}{2}$,EN是△ACF的中位线。
∴EN=$\frac{1}{2}$ =$\frac{9}{2}$,CN=$\frac{1}{2}$CF=6.
∴BN=BC−CN=24−6=18o
在Rt△BEN中,BN=18,EN=$\frac{9}{2}$,
∴BE= $\sqrt{BN²+EN2}$=/18²+ $\sqrt{(\frac{9}{2}}$=$\frac{9\sqrt{17}}{2}$。
∵SABC=2SABE,
∴$\frac{1}{2}$F.BC=2x$\frac{1}{2}$BE.AK。
$\frac{1}{2}$F.BC$\frac{1}{2}$x9×24
∴AK= BE = =$\frac{24\sqrt{17}}{17}$。
$\frac{9\sqrt{17}}{2}$
在Rt△ABK中,AB=15,AK=$\frac{24\sqrt{17}}{17}$
∴BK=
√AB²−AK²= $\sqrt{15²−(\frac{24\sqrt{17}}{17}}$257 $\sqrt{17}$o
∵∠BKM=∠BNE=90°,∠MBK=∠EBN.
∴△BMK∽△BEN
57
∴$\frac{MK}{EN}$=$\frac{BM}{BE}$=$\frac{BK}{BN}$,即$\frac{MK}{9}$=$\frac{BM}{9\sqrt{17}}$=$\frac{17}{18}$
2 2 .,.MK=$\frac{57\sqrt{17}}{68}$,BM=$\frac{57}{4}$
∴AM=AK+MK=2417$\sqrt{17}$567√81794√17
∵PQ⊥BE,AM⊥BE,
∴PQ//AM。
∴$\frac{BP}{AB}$=$\frac{BQ}{BM}$,即$\frac{15−t}{15}$=$\frac{2t}{57}$。
4
解得t=$\frac{285}{59}$
∴当t=$\frac{285}{59}$时,PQ⊥BE。
解:
(1)由题意,得AP=t,BQ=2t。
∴BP=15−t,CQ=24−2t。
∵点P以每秒1个单位长度的速度由点A出发沿AB方向向点B移动,亠:.当点P由点A移动到点B时,所用时间为tA=15÷1=15(s)。
∵点Q以每秒2个单位长度的速度由点B出发沿
BC方向向点C移动,
∴当点Q由点B移动到点C时,所用时间为tB=24÷2=12(s)。
∵当点P或点Q任意一点到达终点时,另一点停止移动,
∴运动时间t的取值范围为0<t≤12。
∵PQ//AC,
∴$\frac{BP}{AB}$=$\frac{BQ}{BC}$,即$\frac{15−t}{15}$=$\frac{2t}{24}$。
解得t=$\frac{20}{3}$。
∴当t=$\frac{20}{3}$时,PQ//AC。
(2)存在某一时刻t,使得△PCQ的面积为6。理由如下:
如图1,过点A作AF⊥BC于点F,过点P作PH⊥BC于点H。

∴AF//PH。
∴△BPH∽△BAF。
∴$\frac{PH}{AF}$=$\frac{BP}{BA}$。
∴.AB=AC,AF⊥BC,BC=24,
.BF=CF=$\frac{1}{2}$BC=12。
在Rt△ABF中,AB=15,BF=12,
= $\sqrt{AB²−BF²}$= $\sqrt{15²−122}$=9。
彐 15−t
“15°
.,PI=9−3o
.,PI.S△PCQ=6,
1C ,即$\frac{1}{2}$(24−2t)(9−)=66
t7。
<t
∴t=10。
∴当t=10时,△PCQ的面积为6。
(3)存在某一时刻t,使得PQ⊥BE。
如图2,过点A作AF⊥BC于点F,作AM⊥BE,交BE于点K,交BC于点M,过点E作EN⊥BC 于点N。

∴EN//AF。
由
(2),知AF=9,BF=CF=12,
∵E是AC的中点,AC=15,
∴AE=EC=$\frac{1}{2}$C=$\frac{15}{2}$,EN是△ACF的中位线。
∴EN=$\frac{1}{2}$ =$\frac{9}{2}$,CN=$\frac{1}{2}$CF=6.
∴BN=BC−CN=24−6=18o
在Rt△BEN中,BN=18,EN=$\frac{9}{2}$,
∴BE= $\sqrt{BN²+EN2}$=/18²+ $\sqrt{(\frac{9}{2}}$=$\frac{9\sqrt{17}}{2}$。
∵SABC=2SABE,
∴$\frac{1}{2}$F.BC=2x$\frac{1}{2}$BE.AK。
$\frac{1}{2}$F.BC$\frac{1}{2}$x9×24
∴AK= BE = =$\frac{24\sqrt{17}}{17}$。
$\frac{9\sqrt{17}}{2}$
在Rt△ABK中,AB=15,AK=$\frac{24\sqrt{17}}{17}$
∴BK=
√AB²−AK²= $\sqrt{15²−(\frac{24\sqrt{17}}{17}}$257 $\sqrt{17}$o
∵∠BKM=∠BNE=90°,∠MBK=∠EBN.
∴△BMK∽△BEN
57
∴$\frac{MK}{EN}$=$\frac{BM}{BE}$=$\frac{BK}{BN}$,即$\frac{MK}{9}$=$\frac{BM}{9\sqrt{17}}$=$\frac{17}{18}$
2 2 .,.MK=$\frac{57\sqrt{17}}{68}$,BM=$\frac{57}{4}$
∴AM=AK+MK=2417$\sqrt{17}$567√81794√17
∵PQ⊥BE,AM⊥BE,
∴PQ//AM。
∴$\frac{BP}{AB}$=$\frac{BQ}{BM}$,即$\frac{15−t}{15}$=$\frac{2t}{57}$。
4
解得t=$\frac{285}{59}$
∴当t=$\frac{285}{59}$时,PQ⊥BE。
查看更多完整答案,请扫码查看


