《2025年考前示范卷九年级数学全一册人教版》

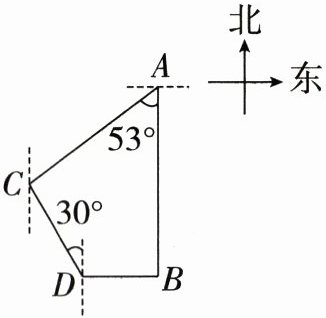
20. (8分)如图,某小区有南北两个门,北门A在南门B的正北方向,小红自小区北门A处出发,沿南偏西53°方向前往小区居民活动中心C处;小强自南门B处出发,沿正西方向行走300m到达D 处,再沿北偏西30°方向前往小区居民活动中心C处与小红汇合,两人所走的路程相同,求该小区北门A与南门B之间的距离。(结果保留整数,参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3,$\sqrt{3}$≈1.73)
　　　

答案：
解:如图，作$CE⊥AB$于点E，过点D作$DF⊥CE$于点F。

由题意，得$EF = BD = 300m$，$BE = DF$。
在$Rt△DCF$中，设$CF = xm$，
则$CD = 2xm$，$FD = \sqrt{3}xm$。
∵小红和小强所走路程相同，
∴$AC = BD + DC = (300 + 2x)m$。
在$Rt△ACE$中，$sin∠CAE = \frac{CE}{AC}$，
∵$CE = CF + FE = x + 300$，
∴$\frac{x + 300}{300 + 2x} = 0.8$。解得$x = 100$。
∴$DF = BE = 100\sqrt{3}m$，$CE = 400m$，$AC = 500m$。
∴$AE = \sqrt{AC^2 - CE^2} = 300m$。
∴$AB = AE + BE = 300 + 100\sqrt{3}≈473(m)$。
∴该小区北门A与南门B之间的距离约为473m。

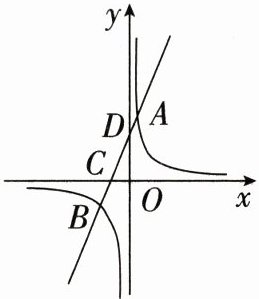
21. (8分)如图,一次函数y=kx+b的图象与反比例函数y=$\frac{−6m}{x}$的图象相交于点A(m+2,6)和点B (−3,m−1),与x轴交于点C,与y轴交于点D。
　(1)求反比例函数与一次函数的表达式;
　(2)根据图象,直接写出$\frac{−6m}{x}$＜kx+b＜0的解集。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 解:
(1)
∵点A(m + 2, 6)在反比例函数$y = \frac{- 6m}{x}$图象上，
∴$- 6m = 6(m + 2)$。解得$m = - 1$。
∴反比例函数的表达式为$y = \frac{6}{x}$，点A(1, 6)，B(- 3, - 2)。
把点A(1, 6)，B(- 3, - 2)代入一次函数的表达式$y = kx + b$，得$\begin{cases}k + b = 6\\- 3k + b = - 2\end{cases}$。解得$\begin{cases}k = 2\\b = 4\end{cases}$。
∴一次函数的表达式为$y = 2x + 4$。
(2)在一次函数$y = 2x + 4$中，令$y = 0$，得$2x + 4 = 0$。解得$x = - 2$。
∴点C(- 2, 0)。
观察图象，$\frac{- 6m}{x}＜kx + b＜0$的解集是$- 3＜x＜ - 2$。

22. (8分)在探究图形变化规律的过程中,结合数学知识之间的内在联系,通过类比、迁移,可以获得宝贵的数学经验。　
[探究1]
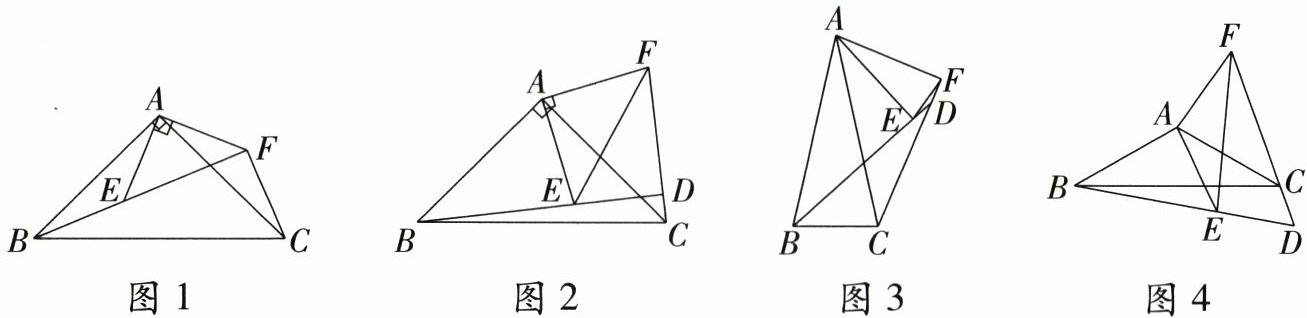
　如图1,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,点B,E,F在同一条直线上,则∠BFC的度数为________　　
[探究2]
　如图2,△ABC和△AEF均为等腰直角三角形,∠BAC=∠EAF=90°,连接BE,CF,延长BE交CF 于点D,则∠BDC的度数为________;
[探究3]
　如图3,△ABC和△AEF均为等腰三角形,AB=AC,AE=AF,连接BE,CF,延长BE交CF于点D。若∠BAC=∠EAF=m°,则∠BDC的度数为________(用含m的式子表示);　
[探究4]
　如图4,△ABC和△AEF均为等腰三角形,AB=AC,AE=AF,连接BE,CF,延长BE交FC的延长线于点D。若∠BAC=∠EAF=120°,则∠BDC的度数为________。
　　　　　　　　　

答案： 解:[探究1]
∵$∠BAC = ∠EAF = 90°$，
∴$∠BAC - ∠CAE = ∠EAF - ∠CAE$，即$∠BAE = ∠CAF$。
∵$△ABC$与$△AEF$均为等腰直角三角形，
∴$AB = AC$，$AE = AF$。
∴$△BAE ≌ △CAF(SAS)$。
∴$∠ABE = ∠ACF$。
∴$∠BFC = 180° - ∠CBF - ∠ACB - ∠ACF = 180° - (∠ABC + ∠ABF) - ∠ACB + ∠ABF = 90°$。
故答案为90°。
[探究2]
∵$∠BAC = ∠EAF = 90°$，
∴$∠BAC - ∠CAE = ∠EAF - ∠CAE$，
即$∠BAE = ∠CAF$。
∵$△ABC$与$△AEF$均为等腰直角三角形，
∴$AB = AC$，$AE = AF$。
∴$△BAE ≌ △CAF(SAS)$。
∴$∠ABE = ∠ACF$。
∴$∠BDC = 180° - ∠CBD - ∠ACB - ∠ACD$
$= 180° - (∠CBD + ∠ACD) - ∠ACB$
$= 180° - (∠CBD + ∠ABD) - ∠ACB$
$= 90°$。
故答案为90°。
[探究3]同[探究2]，得$△BAE ≌ △CAF(SAS)$。
∴$∠ABE = ∠ACF$。
∴$∠BDC = 180° - ∠CBD - ∠ACB - ∠ACD$
$= 180° - (∠CBD + ∠ABD) - ∠ACB$
$= 180° - ∠ABC - ∠ACB$
$= ∠BAC = m°$。
故答案为m°。
[探究4]
∵$∠BAC = ∠EAF = 120°$，
∴$∠BAC - ∠CAE = ∠EAF - ∠CAE$，
即$∠BAE = ∠CAF$。
∵$△ABC$与$△AEF$均为等腰三角形，
∴$AB = AC$，$AE = AF$。
∴$△BAE ≌ △CAF(SAS)$。
∴$∠ABE = ∠ACF$。
∴$∠BDC = ∠ACB + ∠ACF - ∠CBD = ∠ACB + (∠ABE - ∠CBD) = ∠ACB + ∠ABC = 180° - ∠BAC = 60°$。
故答案为60°。