《2025年考前示范卷九年级数学全一册人教版》

25.(10分)小林同学是一名羽毛球运动爱好者,下面是他对击球线路的分析。如图,在平面直角坐标系中,点A,C在x轴上,球网AB与y轴的水平距离0A=3m,CA=2m,AB=1.55m,击球点P 在y轴上。若选择扣球,羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系y1=−0.4x+2.8;若选择吊球,羽毛球的飞行高度y2(m)与水平距离x(m)近似满足二次函数关系,此时,当羽毛球飞行的水平距离是1m时,达到的最大高度为3.2m。
　　(1)求吊球时羽毛球满足的二次函数的表达式;
　　(2)请通过计算说明两种击球方式是否过网;
　　(3)要使球的落地点到点C的距离更近,请通过计算判断应该选择哪种击球方式。
　　　　

答案： 解:
(1)由题意，得二次函数的顶点为(1,3.2)。
∴设二次函数的表达式为y₂=a(x−1)²+3.2。
∵一次函数的表达式y₁=−0.4x+2.8,
　
∴令x=0,得y=2.8。
　　点P(0,2.8)。
　　将点P(0,2.8)代入二次函数表达式，
　　得a+3.2=2.8。
　　解得a=−0.4。
　
∴吊球时羽毛球满足的二次函数的表达式为y₂ = - 0.4(x−1)²+3.2。
(2)令x=3,
　　一次函数y₁=−0.4×3+2.8=1.6,
　　二次函数y₂=−0.4×(3−1)²+3.2=1.6。
　
∵球网AB的高度为1.55m,1.55＜1.6,
∴两种击球方式均能过网。
令y₁ = 0，得0 = - 0.4x + 2.8，解得x = 7。
在二次函数y₂=−0.4(x−1)²+3.2中,令y = 0,得0 = - 0.4(x−1)²+3.2。解得x = 3或 - 1(不符合题意，舍去)。
∵OC=OA+AC=5m,
∴|7−5|=2,|3−5|=2。
∴要使球的落地点到点C的距离更近，应该选择吊球方式。

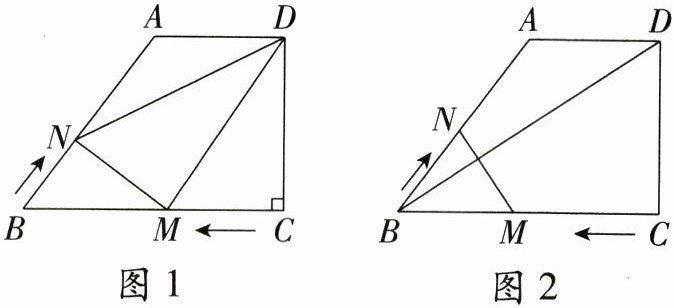
26.(10分)如图1,在四边形ABCD中,AD//BC,DC⊥BC,AD=6cm,DC=8cm,BC=12cm。动点M 在CB上运动,从点C出发运动到点B,速度为每秒2cm;动点N在BA上运动,从点B出发到点A,速度为每秒1cm。两个动点同时出发,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t(s)。
　　(1)当t为何值时,△BMN是直角三角形？
　　(2)设△DMN的面积为S,求S与t之间的函数表达式;
　　(3)如图2,连接BD,是否存在某一时刻t,使MN与BD互相垂直?若存在,求出此时的t值;若不存在,请说明理由。

答案：
解:
(1)如图1,过点A作AE⊥BC于点E。
　根据题意,得AE=DC=8cm,EC=AD=6cm。
∴BE=BC−EC=6cm,BN=tcm,BM=(12−2t)cm。
　在Rt△ABE中,由勾股定理，
　得AB=$\sqrt{AE²+BE²}$=$\sqrt{8²+6²}$=10cm。
　　　　　　　
　若△BMN是直角三角形，有两种情况，分别为∠BMN=90°和∠BNM=90°,分类讨论如下:
①若∠BMN=90°,
∴cosB=$\frac{BM}{BN}$=$\frac{BE}{BA}$=$\frac{6}{10}$=$\frac{3}{5}$。
∴$\frac{12−2t}{t}$=$\frac{3}{5}$。
　解得t=$\frac{60}{13}$。
　②当∠BNM=90°时,
　cosB=$\frac{BN}{BM}$=$\frac{t}{12−2t}$=$\frac{3}{5}$,
　解得t=$\frac{36}{11}$。
　综上所述，当t为$\frac{60}{13}$或$\frac{36}{11}$时,△BMN是直角三角形。
(2)由题意,得CM=2tcm,BN=tcm,BM=(12−2t)cm。
　　　　　　　　　　　　　　　如图1,过点N作NH⊥BC于点H。在Rt△BNH中,cosB=$\frac{BH}{BN}$=$\frac{3}{5}$，
∴BH = $\frac{3}{5}$tcm。
　由勾股定理,得NH = $\frac{4}{5}$tcm。
S△DMN=S梯形ABCD−S△CDM−S△BMN−S△ADN
　　　　　　=$\frac{1}{2}$(AD + BC)·CD - $\frac{1}{2}$×CM·CD - $\frac{1}{2}$×BM×NH - $\frac{1}{2}$AD·(CD - NH)
　　　　　　=$\frac{1}{2}$×(6 + 12)×8 - $\frac{1}{2}$×2t×8 - $\frac{1}{2}$×(12 - 2t)×$\frac{4}{5}$t - $\frac{1}{2}$×6×(8 - $\frac{4}{5}$t)
　　　　　　=$\frac{4}{5}$(t - $\frac{13}{2}$)²+$\frac{71}{5}$。
　
　
　
∵点M从点C运动到点B的时间为12÷2 = 6 (s)，点N从点B运动到点A所需的时间为10÷1 = 10(s),依题意,两者取小值6s,
　
　
　
∴S与t之间的函数表达式为S=$\frac{4}{5}$(t - $\frac{13}{2}$)²+$\frac{71}{5}$(0≤t≤6)。
(3)存在某一时刻t,使MN与BD互相垂直。
　　　　　　当MN⊥BD时,∠BMN=∠BDC,
　
　
　
∴tan∠BMN=tan∠BDC=$\frac{BC}{CD}$=$\frac{12}{8}$=$\frac{3}{2}$。
　　　　　　如图2,过点N作NF⊥BC于点F。
　　　　　　　　　　　　
　　　　　　依题意,得NF = $\frac{4}{5}$tcm,MF = BC - CM - BF = 12 - 2t - $\frac{3}{5}$t = (12 - $\frac{13}{5}$t)cm
　　　　　　tan∠BMN = $\frac{NF}{MF}$ = $\frac{\frac{4}{5}t}{12 - \frac{13}{5}t}$ = $\frac{3}{2}$。
　　　　　　解得t = $\frac{180}{47}$＜6,符合题意。
　　　　当t = $\frac{180}{47}$时,MN与BD互相垂直。