《2025年考前示范卷九年级数学全一册人教版》

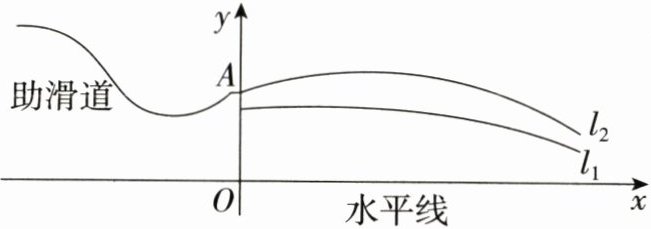
24.(10分)高台跃下,凌空旋转,天际中滑翔出优美的曲线;跳台滑雪简称“跳雪”,运动员沿着助滑道飞速下滑,在起跳点腾空,身体在空中沿抛物线飞行直至着陆坡,主要考核运动员的飞行距离和动作姿势。在这项运动里,我们可以用数学知识解决一些实际问题。如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过起跳点A作水平线的垂线为y轴,建立平面直角坐标系。图中的抛物线l1:y1 = −$\frac{1}{240}$x²+mx + 40近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的点A滑出,滑出后沿一段抛物线l2:y2 = −$\frac{1}{120}$x²+bx + c运动。飞行中某一时刻当运动员运动到离点A处的水平距离为60米时,高出水平线的高度为60米。
　(1)求抛物线l2所对应的函数表达式;
　(2)若运动员在高出水平线10米的小山坡上着地,求此时运动员降落点到点A的水平距离;
　(3)在(2)的条件下,当运动员滑行中与小山坡l1的竖直距离最大时,求运动员运动的水平距离。
　

答案： 解:
(1)由题意，得点A的坐标为(0,50)。
∵抛物线l₂的函数表达式为y₂ = -1/120x² + bx + c，
∴当x = 0时，c = 50。
∴抛物线l₂的函数表达式为y₂ = -1/120x² + bx + 50。
又
∵抛物线l₂过点(60,60)，
∴ -1/120×60² + 60b + 50 = 60。
∴b = 2/3。
∴抛物线l₂所对应的函数表达式为y₂ = -1/120x² + 2/3x + 50。
(2)把y = 10代入l₂，得10 = -1/120x² + 2/3x + 50。
解得x₁ = 120，x₂ = -40(不符合题意，舍去)。
所以此时运动员降落点到点A的水平距离为120米。
(3)
∵运动员在高出水平线10米的小山坡上着地时，运动员落地点距点A的水平距离为120米，
∴点(120,10)在抛物线l₁上。
把点(120,10)代入y = -1/240x² + mx + 40中，
得 -1/240×120² + 120m + 40 = 10。
解得m = 1/4。
∴抛物线l₁的函数表达式为y = -1/240x² + 1/4x + 40。
∴y₂ - y₁ = -1/120x² + 2/3x + 50 + 1/240x² - 1/4x - 40
= -1/240x² + 5/12x + 10
= -1/240(x - 50)² + 21 2/3
∵ -1/240＜0，
∴当x＜50时，y₂ - y₁的值随x值的增大而增大。
∴当x = 50时，运动员滑行中与小山坡l₁的竖直距离最大。
∴此时，运动员运动的水平距离为50米。

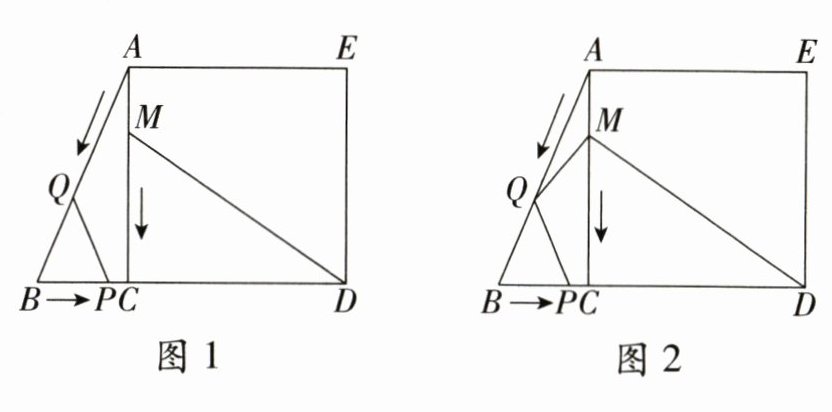
25.(12分)如图1,在Rt△ABC中,BC = 5cm,AC = 12cm,以AC为边作正方形ACDE,点P从点B出发,沿BD方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AB方向匀速运动,速度为2cm/s,点M从点A出发,沿AC方向匀速运动,速度为1cm/s;当一个点停止运动,另外两个点也停止运动。连接PQ,MD。设运动时间为t(s)(0＜t＜6.5),解答下列问题。
　(1)是否存在某一时刻t,使点P在MD的垂直平分线上?若存在,求出t的值;若不存在,说明理由;
　(2)当t为何值时,△BPQ为等腰三角形？
　(3)如图2,连接MQ,设四边形MQPD的面积为y(cm²),求y与t之间的函数表达式;
　(4)当∠BQP = 45°时,求t的值。

答案：
解:
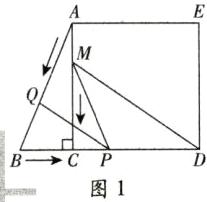
(1)不存在某一时刻t，使点P在MD的垂直平分线上。理由如下:
如图1，由题意，得BP = t cm，AQ = 2t cm，AM = t cm。
在Rt△ABC中，BC = 5cm，AC = 12cm，
∴AB = √(AC² + BC²) = 13cm。
∵正方形ACDE是以AC为边的，

若点P在MD的垂直平分线上，
∴PD = PM。
∵四边形ACDE是正方形，
∴∠PCM = 90°。
在Rt△MCP中，
∵PM² = CM² + CP²，
∴(17 - t)² = (12 - t)² + (t - 5)²。
解得t = 2√30或 - 2√30(不符合题意，舍去)。
∵0＜t＜6.5，
∴t = 2√30不符合题意。
∴不存在某一时刻t，使点P在MD的垂直平分线上。
(2)由
(1)，知AB = 13cm，
由题意，得BP = t cm，AQ = 2t cm，AM = t cm。
∴BQ = (13 - 2t)cm。
若△BPQ为等腰三角形，则有BP = BQ，BQ = PQ，BP = PQ三种情况，分类讨论如下:
①当BP = BQ时，t = 13 - 2t。
解得t = 13/3。
②当BQ = PQ时，如图2，过点Q作QF⊥BC于点F。

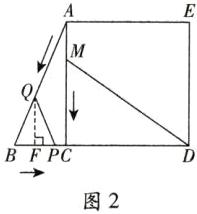
∴BF = FP = 1/2BP = t/2 cm。
∵QF⊥BC，∠ACD = 90°，
∴QF//AC。
∴BQ/BA = BF/BC，即(13 - 2t)/13 = (t/2)/5。
解得t = 130/33。
③当BP = PQ时，如图3，过点P作PG⊥AB于点G。

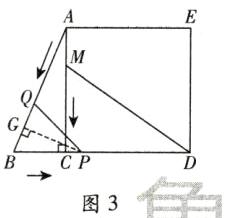
∴BG = 1/2BQ = (13 - 2t)/2 cm
∵∠BGP = ∠BCA = 90°，∠PBG = ∠ABC，
∴△PBG∽△ABC
∴BG/BC = BP/BA，即((13 - 2t)/2)/5 = t/13。
解得t = 169/36。
综上所述，当t = 13/3或130/33或169/36时，△BPQ为等腰三角形。
(3)如图4，过点Q作QG⊥AC于点G，作QH⊥BC于点H。

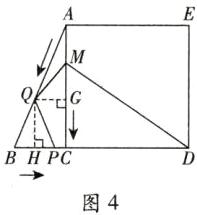
∴QG//BC，QH//AC。
∴QG/BC = AQ/AB，即QG/5 = 2t/13。
∴QG = 10/13t cm。
∵QH//AC，
∴QH/AC = BQ/AB，即QH/12 = (13 - 2t)/13。
∴QH = (156 - 24t)/13 cm。
∴y = S四边形MOPD = S△ABC - S△AMQ - S△BPQ + S△MCD = 1/2×BC×AC - 1/2×AM×QG - 1/2×BP×QH + 1/2×CD×CM = 1/2×5×12 - 1/2×t×10/13t - 1/2×t×(156 - 24t)/13 + 1/2×12×(12 - t) = 7/13t² - 12t + 102。
∴y与t之间的函数表达式为y = 7/13t² - 12t + 102(0＜t＜6.5)。
(4)如图5，过点P作PK⊥AB于点K，过点Q作QH⊥BP于点H。

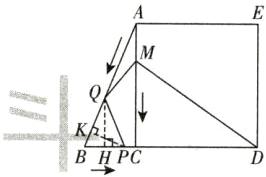
由题意，得AQ = 2t cm，BP = t cm，BQ = (13 - 2t)cm。
∵S△BPQ = 1/2QH×BP = 1/2PK×BQ，
由
(3)，知QH = (156 - 24t)/13 cm，
∴((156 - 24t)/13)×t = PK×(13 - 2t)。
∴PK = 12/13t cm。
在Rt△BPK中，BK² + PK² = BP²，
∴BK² + (12/13t)² = t²。
∴BK = 5/13t cm
∴KQ = AB - AQ - BK = 13 - 2t - 5/13t = (13 - 31/13t)cm
∵∠BQP = 45°，
∴KQ = PK，即13 - 31/13t = 12/13t。
解得t = 169/43。
∴当∠BQP = 45°时，t的值为169/43。