《2025年考前示范卷九年级数学全一册人教版》

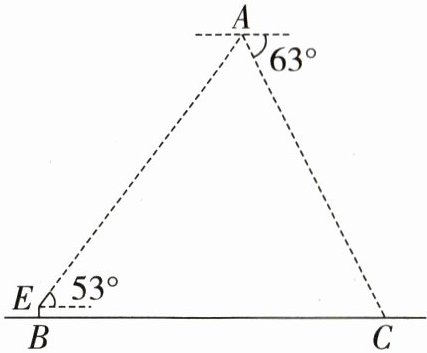
20.(6分)随着科学技术的不断进步,无人机被广泛应用到实际生活中。如图所示,某同学站在广场的B处遥控无人机,他抬头仰视无人机时的仰角为53°,此时从无人机测得广场C处的俯角为63°,若该同学的眼睛到地面的距离BE=1.6m,AE=50m,(点A,E,B,C在同一平面内),求BC 之间的距离。(结果精确到1m,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)

答案：
解:如图,过点A作AF⊥BC,垂足为F,过点E 作EG⊥AF,垂足为G。
　　　　　　　
　　由题意,得EB=GF=1.6m,BF=EG,
　　∠DAC=63°,AD//BC。
　
∴∠DAC=∠ACF=63°。
　　.在Rt△AEG中,AE=50m,∠AEG=53°,
　　coS∠AEG=$\frac{EG}{AE}$,sin∠AEG=$\frac{AG}{AE}$,
=AE.cos53°~50x0.6=30(m),
　　　　　.sin53°≈50×0.8=40(m)。
AF=AG+GF=40+1.6=41.6(m)。
在Rt△ACF中,∠ACF=63°,tan∠ACF=$\frac{AF}{CF}$,
　
∴CF=tanAF　≈$\frac{41.6}{1.96}$≈21.2(m)。
BC=BF+=EG+CF=30+21.2≈51(m)。
　　I..B　之间的距离约为51m。

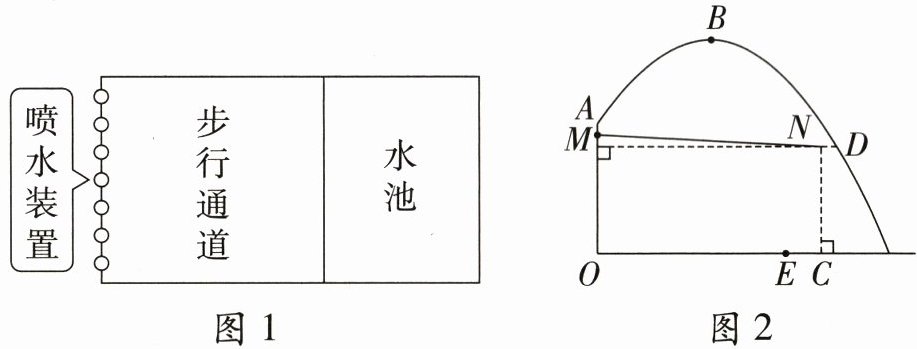
21.(6分)城建部门计划修建一条喷泉步行通道。图1是项目俯视示意图。步行通道的一侧是一排垂直于路面的柱形喷水装置,另一侧是方形水池。图2是主视示意图。喷水装置OA的高度是2米,水流从喷头A处喷出后呈抛物线路径落入水池内。当水流在与喷头水平距离为2米时达到最高点B,此时距路面的最大高度为3.6米。为避免溅起的水雾影响通道上的行人,计划安装一个透明的倾斜防水罩。防水罩的一端固定在喷水装置上的点M处,另一端与路面的垂直高度NC为1.8米,与喷泉水流的水平距离ND为0.3米。点C到水池外壁的水平距离CE为0.6米，求步行通道的宽OE。(结果精确到0.1米,参考数据::$\sqrt{2}$≈1.41)

答案：
解:如图,以点0为坐标原点,0C所在直线为x
轴，oA所在直线为y轴，建立如图所示的平面直角坐标系。
　　　　　　
　由题意知,点A(0,2),点B(2,3.6),
∵抛物线的最高点为B,
∴设抛物线的表达式为y=a(x−2)²+3.6。
　把点A(0,2)代入,得4a+3.6=2。
　解得a=−0.4。
∴抛物线的表达式为y=−0.4(x−2)²+3.6。
　当y=1.8时,−0.4(x−2)²+3.6=1.8。
　解得x=2±3√2°
∵点D在第一象限，
∴xD=2+$\frac{3√2}{2}$。
∴点D的坐标为(2+3,1.8)o
∴OE=xD−DN−CE≈2+$\frac{3×1.41}{2}$−0.3−0.6 ≈3.2(米)。
∴步行通道的宽0E约为3.2米。

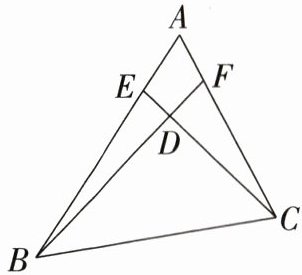
22.(6分)如图,在△ABC中,E,F分别为边AB,AC上的点,BF与CE相交于点D。
(1)若AE=$\frac{1}{4}$AB,AF=$\frac{1}{4}$AC,
①$\frac{ED}{EC}$的值为________;
②△CDF的面积为3,则△ABC的面积为________;
(2)若AE=$\frac{1}{n}$AB,AF=$\frac{1}{n}$AC,S△CDF=________S△ABC(用含n的代数式表示)

答案：
解:
(1)①如图,连接EF。
　　　　　　　
　
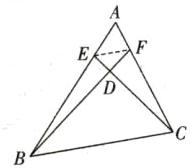
∵AE=$\frac{1}{4}$　,AF=$\frac{1}{4}$C,
　
∴$\frac{AE}{AB}$=$\frac{AF}{AC}$=$\frac{1}{4}$。
　
∴又
∵△A∠EEFA∽F=△∠ABBCAoC,
　
　
　
　
∴∠AEF=∠ABC,$\frac{EF}{BC}$=$\frac{1}{4}$。
　
　
　
∴EF///BC.
∴△EDF∽△CDB。
　
∴$\frac{EF}{CB}$=$\frac{DE}{DC}$=$\frac{1}{4}$o
∴$\frac{ED}{EC}$=$\frac{1}{5}$。　　　　　　故答案为$\frac{1}{5}$。
　　②由①,知△EDF∽△CDB。
∴$\frac{DF}{DB}$=$\frac{EF}{CB}$=$\frac{1}{4}$。
∵S△cDF=3,SS△△cBDDCF=$\frac{DF}{DB}$=$\frac{1}{4}$
∴S△BDC=12。
　
∴S△BCF=S△CDF+S△BDC=3+12=15o
　
∵$\frac{AF}{AC}$=$\frac{1}{4}$，
∴.$\frac{CF}{AC}$=$\frac{3}{4}$。
　
∴SS△△ABCBFC$\frac{CF}{AC}$=$\frac{3}{4}$,
　
∴S△ABC=$\frac{15}{3}$x4=20。
　　故答案为20。
(2)
∵AE=$\frac{1}{n}$　,AF=$\frac{1}{n}$C,
　
∴$\frac{AE}{AB}$=$\frac{AF}{AC}$=$\frac{1}{n}$。
∴$\frac{CF}{AC}$=$\frac{n−1}{n}$。
　　又
∵∠EAF=∠BAC,
　
∴△AEF∽△ABCo
　
∴∠AEF=∠ABC,$\frac{EF}{BC}$H$\frac{1}{n}$。
　
∴EF///BC。
　
∴△EDF∽△CDBo
　
∴$\frac{EF}{CB}$=$\frac{DE}{DC}$=$\frac{DF}{DB}$=$\frac{1}{n}$。
　
∴DB=nDF。
　
∴SS△△CBDCFF=$\frac{DF}{BF}$=$\frac{DF}{DF+DB}$=$\frac{DF}{(n+1)DF}$=$\frac{1}{n+1}$。
　
∴S△BCF=(n+1)S△CDFo
　　.SS△ABCBCF$\frac{CF}{AC}$=$\frac{n−1}{n}$,
　
∴SABC=nn−1S△BCFO
　
∴S△ABC=$\frac{n(n+1)}{n−1}$S△CDFo
　
∴S△CDF=nn²−+1ns△ABCo
　　故答案为$\frac{n−1}{n²+n}$。

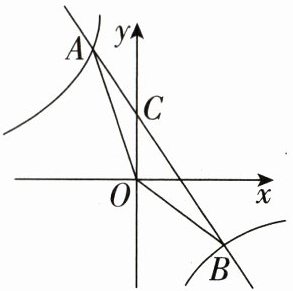
23.(8分)如图,在平面直角坐标系中,一次函数y=ax+b(a＜0)的图象与反比例函数y=$\frac{k}{x}$(k＜0)的图象交于A(−m,3m),B(4,−3)两点,一次函数与y轴交于点C,连接OA,OB。
(1)求反比例函数和一次函数的表达式;
(2)若在第一象限内存在一点P,使得以P,A,O,B为顶点的四边形为平行四边形,请直接写出点P的坐标。

答案：
解:
(1)
∵点B(4,−3)在反比例函数y=$\frac{k}{x}$的图.象
　　..−³=$\frac{k}{4}$。解得k=−12。
..−³=
　
∴反比例函数的表达式为y=−$\frac{12}{x}$。
　　　点　　　　　　　)在反比例函数y=−$\frac{12}{x}$的图象上
∴3m=$\frac{12}{−m}$。
　　解得m1=2,m2=−2(不符合题意,舍去)。
　
∴点A的坐标为(−2,6)。
　
∵点A,B在一次函数y=ax+b(a＜0)的图象上，
∴把点A(−2,6),B(4,−3)分别代入,得{4−a2+ab+=b=−36。'解得ab==3$\frac{3}{2}$。　,
　　　　　　　　{
　
∴一次函数的表达式为y=−3歹x+3。
(2)如图，P为第一象限内任意一点，连接0P，交AB于点M,连接AP,BP。
　　　　　　　
∵四边形AOBP是平行四边形，
∴AM=BM,OM=PM。
　...点A(−2,6),B(4,−3),
∴点M(1,$\frac{3}{2}$)。
　,.点0(0,0)。
∴$\frac{0+x,}{2}$=1,$\frac{O+yp}{2}$=$\frac{3}{2}$。
∴xp=2,yp=3。
∴点P的坐标为(2,3)。